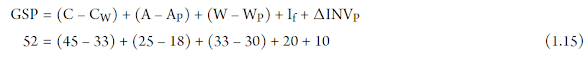Fluxos e Estoques de Produção nas Contas Nacionais - Anwar Shaikh

APÊNDICE 4.1 - Fluxos e Estoques de Produção nas Contas Nacionais (Shaikh, 2016)

1. Uma Estrutura para Monitorar Fluxos e Estoques de Produção

1. As contas clássicas concentram-se na produção concluída (XP) (ou seja, bens acabados) [1]. Já as contas convencionais enfocam a produção iniciada (X), que é a soma dos produtos acabados e semiacabados. Essa diferença no conceito de produção total gera outras diferenças nas medidas de insumos intermediários, custos salariais e valor adicionado, embora, no final, ambas as contas resultem na mesma medida de lucro bruto. O mapeamento entre as contas clássicas e as contas padrão será realizado a seguir no nível de uma economia privada fechada com apenas trabalho produtivo, pois é nesse ponto que surgem as diferenças fundamentais. A análise pode ser facilmente estendida para incluir os setores governamental e externo. A incorporação do trabalho não produtivo é tratada detalhadamente em Shaikh e Tonak (1994). Valores numéricos ilustrativos consistentes com a tabela 4.2 do texto deste capítulo são adicionados a todas as variáveis.

[1]: “O processo anual de reprodução é facilmente compreendido, desde que tenhamos em vista apenas o total da produção do ano. Mas cada componente individual desse produto deve ser levado ao mercado como mercadoria” (Marx 1967a, cap. 24, sec. 2, 590). “Os produtos acabados, seja qual for sua forma material ou seu valor de uso, seu efeito útil, são aqui todos capital-mercadoria” (Marx 1967b, cap. 10, 205).

2. É útil começar pelas categorias familiares das contas padrão de renda e produto nacional (NIPA). A produção total é definida como o produto bruto (X), que é a soma dos insumos intermediários adquiridos (A), das vendas de bens finais (XS) e da variação de estoques (ΔINV). A variação de estoques é composta pela soma das variações nos estoques de materiais e suprimentos (ΔINVA), de produtos em processo (ΔINVWIP) e de produtos acabados e bens mantidos para revenda (ΔINVP). Deve-se notar que os produtos acabados incluem materiais, na medida em que representam o produto final dos produtores de materiais, enquanto os bens finais referem-se a produtos acabados que não reentram diretamente na produção (ou seja, bens de consumo e investimento) (BEA 2008, 2–2, 2–9, 2–10) [2]. Para distinguir entre as duas categorias, indicarei os produtos acabados (ou seja, produzidos) com o subscrito “P” e os bens finais com o subscrito “F”. Assim, dentro da medida de produto bruto, a soma dos dois primeiros itens, insumos intermediários adquiridos (vendidos) e vendas de bens finais, representa o total das vendas de produtos acabados. Por fim, o valor adicionado bruto (GVA) e o produto interno bruto (PIB) são definidos como o produto bruto menos os insumos intermediários. Como o produto bruto pode sempre ser expresso pelo lado das fontes como a soma de seus custos com materiais (A), custos salariais (W) e lucro bruto, o GVA é a soma dos custos salariais e do lucro bruto. Pelo lado dos usos, o produto bruto é a soma das vendas (ou compras) de materiais (A) e das vendas finais de bens de consumo (C), bens de investimento fixo (If) e variações de estoques. Portanto, o produto interno bruto (PIB) é a soma do consumo, do investimento fixo e da variação total dos estoques de materiais, produtos em processo e bens finais. Devido ao seu foco na produção iniciada, a medida de “produto final” das NIPA tem a curiosa característica de englobar acréscimos aos estoques de matérias-primas e itens parcialmente fabricados (Shapiro 1966, 26n11).

[2]: Vendas finais são as “vendas da indústria para os usuários finais” e equivalem à soma das despesas de consumo pessoal, do investimento fixo privado bruto, das despesas de consumo do governo e do investimento bruto, e das exportações líquidas de bens e serviços (BEA 2008, 2–10, 12–12).

3. Para realizar a transição para as categorias clássicas, é necessário extrair categorias relevantes para os bens acabados (isto é, produzidos). Observamos no início deste apêndice que as vendas de bens acabados correspondem à soma dos insumos intermediários adquiridos (A) e das vendas de bens finais (FS). Como a produção concluída aumenta os estoques de bens acabados e as vendas de bens acabados reduzem esses estoques, a variação nesses estoques (ΔINVP) é a diferença entre a produção total de bens acabados (XP) e as vendas totais de bens acabados (A + FS). Essa relação pode ser escrita como:

4. As equações (1.1), (1.2) e (1.6) indicam que a medida padrão de produção iniciada é maior do que a medida clássica de produto acabado pela soma das variações nos estoques de materiais e produtos em processo.

5. Uma comparação semelhante pode ser feita entre os custos de materiais e trabalho da produção total (A + W) e os custos correspondentes do produto acabado. O custo de materiais dos bens acabados (AP) é o custo de materiais dos bens acabados cuja produção foi iniciada no ano corrente (A'P) mais o custo de insumos dos bens acabados cuja produção foi iniciada em anos anteriores (A''P) [3]. Da mesma forma, o custo de trabalho dos bens acabados (WP) é o custo de trabalho dos bens acabados iniciados no ano corrente (W'P) mais o custo de trabalho dos bens acabados iniciados em anos anteriores (W''P). Também é útil observar que a folha salarial total do ano corrente (W) é a soma dos salários gastos na produção iniciada no ano, tanto a concluída (W'P) quanto a não concluída (WWIP).

[3]: Se os preços estiverem variando, os custos atuais dos insumos não serão os mesmos que os custos efetivamente pagos, o que geralmente é tratado por meio de ajustes de valoração de estoques (BEA 2008, 2-8n19).

6. As variações nos estoques de materiais e produtos em processo fornecem os elos que faltam entre as medidas convencional e clássica de custo total. A variação nos estoques de materiais (ΔINVA) é a diferença entre as compras de materiais (A), que aumentam esses estoques, e seu uso na produção iniciada e concluída dentro do ano (A'P) e na produção em processo (AWIP). A variação nos estoques de produtos em processo (ΔINVWIP) decorre da adição de novos produtos em processo, avaliados a custo (AWIP + WWIP), e da subtração dos custos dos bens atuais iniciados em anos anteriores (AWIP + WWIP), que saem desses estoques ao serem concluídos.

7. Agora estamos em posição de demonstrar que as duas medidas de custos de produção diferem exatamente pelo mesmo valor que as medidas correspondentes de produto total [4]. Segue-se imediatamente que a medida de lucro bruto é a mesma em ambos os casos: a medida padrão do excedente operacional bruto (GOS) é igual à medida clássica da forma monetária do excedente bruto de valor (GSV). Portanto, o termo lucro bruto (PG) é usado para ambas.

[4]: A combinação das equações (1.8)–(1.12) resulta em:

8. A medida clássica do excedente bruto também possui um equivalente pelo lado do uso, que é o produto do excedente bruto (GSP). Este é a diferença entre o produto total acabado (XP) e os equivalentes de uso de seus custos (AP + WP). A partir das equações (1.1) e (1.6), a forma de uso do produto total acabado é XP = A + C + If + ΔINVP; AP já está na forma de uso; e, assumindo que o consumo dos trabalhadores é igual aos seus salários, os salários dos trabalhadores utilizados para criar o produto total podem ser escritos como WP = W – (W–WP) = CW – (W–WP), onde CW é o consumo corrente dos trabalhadores. Assim, com uma pequena reorganização dos termos, obtemos:

9. O primeiro termo entre parênteses no lado direito é o consumo dos capitalistas, que é a diferença entre o consumo total e o consumo dos trabalhadores. O segundo termo é a diferença entre os insumos adquiridos no ano corrente e aqueles utilizados na produção do produto final, representando o investimento total em materiais. O terceiro termo é a diferença entre as aquisições atuais de força de trabalho e aquelas realizadas na produção de bens acabados, representando o investimento total em força de trabalho. A soma do investimento em materiais e em força de trabalho constitui o investimento total em capital circulante (Ic) [5]. Como a produção leva tempo, o aumento da produção só pode ser alcançado primeiro pelo aumento dos insumos via investimento circulante. O investimento fixo (If), por outro lado, expande a capacidade. A distinção entre os dois é essencial para a dinâmica clássica (capítulos 12–13). Assim, o produto do excedente bruto é a soma do consumo dos capitalistas (CC), do investimento em capital circulante, do investimento em capital fixo e das variações nos estoques de bens finais. Isso é exatamente o que aparece nos esquemas de reprodução de Marx [6].

[5]: Marx afirma que o capital circulante é composto pelos salários e pelos materiais brutos e auxiliares consumidos na produção de uma mercadoria. O investimento em capital circulante é o aumento desse montante (Marx, 1967b, cap. 12, 231, 236).

[6]: Nos esquemas de reprodução de Marx, no caso apenas de capital circulante, em sua notação, a forma de uso do valor excedente total é S = Sc + Sac + Sav, onde S = valor excedente líquido, Sc = consumo dos capitalistas, Sac = ΔC = investimento em capital circulante, e Sav = ΔV = investimento em capital variável (Sweezy 1942, 162–163). A reprodução simples ocorre quando não há crescimento, de modo que ΔC = ΔV, caso em que todo o valor excedente é destinado ao consumo dos capitalistas (S = Sc).

10. Agora podemos comparar as medidas padrão e clássica de valor adicionado bruto [7]. Como ambas incorporam a mesma medida de lucro bruto (GOS = GSV = PG), a diferença só pode surgir das diferenças na medida de salários. E, como observamos anteriormente, essa diferença (W – WP) é simplesmente o investimento em força de trabalho. Esse é exatamente o ponto levantado por Tsuru (1942, 371–373) [8], embora sua derivação se refira ao caso especial de capital puramente circulante com um período de produção uniforme (veja capítulo 4, nota 15).

[7]: Uma notação ligeiramente diferente para o valor adicionado bruto clássico foi usada em Shaikh e Tonak (1994, cap. 3).

[8]: Tsuru também argumenta que a variação na folha salarial aparece duas vezes na medida convencional de produto interno bruto. Isso é melhor entendido agrupando sua medida em três itens: VA-NIPA = (Sc) + (V + Sav) + (Sac + Sav). O primeiro item é o consumo dos capitalistas. O segundo é o consumo dos trabalhadores: como toda produção leva um ano, o custo do trabalho de bens acabados (V) é a folha salarial do ano anterior, V + Sav = V + ΔV = a folha salarial do ano atual, e esta última é igual ao consumo atual dos trabalhadores, dada a suposição de Tsuru e Marx de que toda renda salarial é consumida no mesmo período. O terceiro item é o investimento total em capital circulante, ou seja, o acréscimo líquido aos estoques de produtos em processo, medido pelo custo dos materiais adicionais (Sac = ΔC) e do trabalho adicional (Sav = ΔV). Assim, VA-NIPA = Consumo Total + Investimento Total. De fato, um aumento na folha salarial aparece tanto no consumo atual dos trabalhadores quanto como parte do acréscimo atual aos estoques de produtos em processo.

11. Por fim, pode-se demonstrar que é possível identificar explicitamente o investimento em capital circulante mesmo dentro das medidas de produto bruto e produto interno bruto (PIB) das NIPA. O produto bruto é a soma das compras de materiais (A) e do produto interno bruto, sendo este último a soma do consumo (C), dos bens de investimento fixo (If) e das variações de estoques (ΔINV). Este último item corresponde à variação nos estoques de bens finais (ΔINVP) mais a soma da variação nos estoques de materiais e suprimentos e produtos em processo (ΔINVA + ΔINVWIP). Contudo, pela equação (1.13), essa última soma é simplesmente o investimento em capital circulante.

12. Segue-se que, a partir das equações (1.2), (1.5) e (1.20), podemos expressar o produto interno bruto (PIB) das NIPA como:

13. O investimento em capital circulante está presente o tempo todo, escondido à vista de todos.

Siglas:

A = insumos intermediários adquiridos (custos materiais)

AP = custo de materiais dos bens acabados (AP = A'P + A''P)

(A’P) = custo de materiais dos bens acabados cuja produção foi iniciada no ano corrente 

(A’’P) = custo de insumos dos bens acabados cuja produção foi iniciada em anos anteriores 

(AWIP) = custo de materiais na produção em processo

C = bens de consumo

CC = consumo dos capitalistas

F = bens finais;

FS = vendas finais

GVA = valor adicionado bruto (convencional)

GVAP = Valor Adicionado Bruto Clássico

GOS = medida padrão do excedente operacional bruto

GSP = produto excedente bruto

GSV = medida clássica da forma monetária do excedente bruto de valor

If = bens de investimento fixo

Ic = investimento em capital circulante

NIPA = contas padrão de renda e produto nacional

P = produtos acabados (ou seja, produzidos)

PG = lucro bruto

PIB = produto interno bruto

W = custos salariais

WP = custo de trabalho dos bens acabados (WP = W'P + W''P)

(W’P) = custo salarial dos bens acabados iniciados no ano corrente

(W’’P) = custo salarial dos bens acabados iniciados em anos anteriores

(WWIP) = salários gastos na produção iniciada no ano e não concluída 

X = produto bruto (produção iniciada = produtos acabados + semiacabados)

XP = produção total de bens acabados (produção concluída)

XS = vendas de bens finais

(ΔINV) = variação de estoques

(ΔINVA) = variações nos estoques de materiais e suprimentos

(ΔINVWIP) = variações nos estoques de produtos em processo 

(ΔINVP) = variações nos estoques de produtos acabados e bens mantidos para revenda

Desigualdade e Movimento da Taxa de Câmbio em Macroeconomia Aberta - Carnevali et al.

CARNEVALI, Emilio; RUGGERI, Francesco; VERONESE PASSARELLA, Marco. Inequality and Exchange Rate Movements in an Open-Economy Macroeconomic Model. Review of Political Economy, v. 36, n. 2, p. 722–760, 2024. DOI: 10.1080/09538259.2022.2062961.

SUMÁRIO

1. Introdução  

2. O Contexto: Financeirização  

    2.1. Mudanças na Distribuição de Renda  

    2.2. Financeirização das Empresas  

    2.3. Liberalização Financeira e Consumo Financiado por Dívidas  

    2.4. Liberalização da Taxa de Câmbio e da Conta de Capital  

    2.5. Desenvolvimento Financeiro  

    2.6. Regimes de Crescimento Baseados em Dívidas vs Baseados em Exportações  

3. Revisão da Literatura  

4. O Modelo  

    4.1. O Setor Doméstico  

    4.2. Consumo e Renda Total  

    4.3. O Setor Financeiro  

    4.4. O Mecanismo da Taxa de Câmbio  

5. Apresentação dos Resultados  

    5.1. Crescimento Baseado em Dívidas Privadas e Desigualdade  

    5.2. Consequências Econômicas da (Crescente) Desigualdade  

6. Evidências dos Estados Unidos  

7. Conclusão

RESUMO

Este artigo apresenta um modelo macroeconômico completo (SFC) para estudar a distribuição de renda e riqueza em uma economia aberta. Argumentamos que as taxas de câmbio e o estoque de dívida externa desempenham um papel crucial na determinação da desigualdade entre e dentro dos países. Usando a "hipótese da renda relativa", mostramos que o consumo financiado por dívida de famílias de baixa renda pode afetar tanto a renda total quanto a renda disponível de famílias de alta renda no médio prazo. Além disso, embora uma maior desigualdade seja prejudicial à economia doméstica, ela pode beneficiar os parceiros comerciais.

INTRODUÇÃO

A relação entre finanças e desigualdade tem atraído crescente atenção desde o início da crise financeira dos Estados Unidos em 2007–08. O tema tem sido frequentemente enquadrado no conceito mais amplo de "financeirização".  

A maioria dos estudos foca em países ou regiões isolados. Como resultado, o papel dos fluxos de capital entre países e das taxas de câmbio é geralmente negligenciado. Apresentamos um modelo de economia aberta, denominado IEROE (Inequality and Exchange Rate in the Open Economy), que busca preencher essa lacuna na pesquisa. Sua estrutura básica é derivada do modelo OPENFLEX, desenvolvido por Godley e Lavoie (2007). O modelo de referência foi ampliado com três blocos de equações. As novas características são as seguintes: (1) o setor doméstico de famílias é dividido em dois grupos, com base na renda mediana; (2) as famílias de baixa renda tentam emular os padrões de consumo das famílias de alta renda (hipótese da renda relativa, RIH); e (3) o crédito ao consumo das famílias de baixa renda é financiado por empréstimos bancários.  

O artigo está organizado da seguinte forma. A Seção Dois apresenta o conceito de "financeirização" e fornece evidências de como ele tem sido usado para resumir uma série coerente de "mudanças estruturais socioeconômicas". A Seção Três apresenta uma revisão da literatura sobre as contribuições mais recentes em finanças e desigualdade. A estrutura do modelo é discutida em detalhe na Seção Quatro. Na Seção Cinco, utilizamos o modelo para testar o impacto do comportamento emulativo e de uma mudança na distribuição primária de renda, respectivamente. Mostramos (experimento 1) que o comportamento emulativo das famílias de baixa renda (financiado por empréstimos bancários) tem um impacto negativo no médio prazo sobre a renda total doméstica. Além disso, afeta a renda e a riqueza financeira líquida da classe alta. Uma distribuição mais desigual de renda (experimento 2) é prejudicial para o país como um todo. Contudo, pode beneficiar tanto as famílias domésticas de alta renda quanto os parceiros comerciais. Na Seção Seis, mostramos que os resultados do modelo replicam as séries temporais disponíveis para a economia dos EUA durante a crise de 2007–08. De forma mais geral, nossos experimentos elucidam as principais relações causais entre o aumento da desigualdade de renda e riqueza e a instabilidade financeira em uma economia aberta. Isso também pode ser muito útil na economia da pandemia de Covid-19, já que evidências indicam que o recente choque econômico contribuiu para um aumento adicional no nível de desigualdade entre países (Bottan, Hoffmann e Vera-Cossio, 2020; Nassif-Pires et al., 2020; Qureshi, 2020; Perry, Aronson e Pescosolido, 2021). Planos de recuperação pós-pandemia devem levar essa lição em conta se desejam contribuir para uma economia mais estável e resiliente. Observações finais são apresentadas na Seção Sete.  

2. O Contexto: Financeirização

O termo "financeirização" é frequentemente usado para marcar o período desde o final da década de 1970 até o surgimento da crise de 2007–08. Muitos autores têm empregado o termo para explorar diversos aspectos das economias avançadas desde então, mas, como observa Krippner (2005, p. 181), "a literatura sobre financeirização é, no momento, um campo um tanto livre, carecendo de uma visão coesa sobre o que deve ser explicado". De fato, mais de 15 anos depois, ainda falta uma interpretação única desse conceito na literatura econômica.  

De acordo com Epstein (2019, p. 380), a financeirização "refere-se à crescente importância dos mercados financeiros, dos motivos financeiros, das instituições financeiras e das elites financeiras no funcionamento da economia e de suas instituições governantes, tanto no nível nacional quanto internacional". Essa definição é suficientemente geral para incluir uma variedade de mudanças estruturais que ocorreram na maioria das economias avançadas. Nas próximas subseções, discutimos brevemente algumas das mudanças mais relevantes.  

2.1. Mudanças na Distribuição de Renda

Durante a era da financeirização, a distribuição de renda favoreceu o capital em detrimento do trabalho (ver Hein e Dodig, 2015, para uma análise de longo prazo desse fenômeno). A Figura 1 mostra a evolução da distribuição funcional da renda em economias selecionadas. A Figura 2 foca na participação da renda do 1% mais rico.  

Todos os países registraram uma redução na participação salarial desde o final da década de 1970. A maior parte dessa "redistribuição" ocorreu durante os anos 1980. Ao mesmo tempo, os rendimentos do 1% mais rico registraram um crescimento substancial. Essa redistribuição de renda de baixo para cima começou no início dos anos 1980 nos EUA e no Reino Unido, onde Ronald Reagan e Margaret Thatcher lideraram a "revolução conservadora" no mundo ocidental. Na Espanha, Alemanha, Suécia e França, esse processo de redistribuição começou apenas em meados da década de 1990 ou até mesmo no início dos anos 2000 (Hein, 2015).  

Figura 1 - Participação do trabalho na renda nacional (%). Países selecionados da OCDE.

Nota: Nossa elaboração com base nos dados da *World Inequality Database*, 2021.  

Figura 2 - Renda nacional antes de impostos, participação do 1% mais rico. Países selecionados da OCDE.

Nota: Nossa elaboração com base nos dados da World Inequality Database, 2021.  

A distribuição mais desigual da renda entre salários e lucros (incluindo dividendos, pagamentos de juros e lucros retidos) foi acompanhada por uma distribuição mais desigual da renda pessoal entre os assalariados (isto é, entre trabalhadores de baixa renda e altos executivos, estrelas do esporte e do entretenimento, e empregados do setor financeiro). A queda no poder de barganha dos sindicatos e a mudança na estrutura da economia contribuíram para a estagnação dos salários reais nas indústrias manufatureiras tradicionais.

2.2. Financeirização das Empresas

As empresas não financeiras aumentaram seus investimentos em portfólios nos mercados de ações e abriram novas subsidiárias financeiras em vez de adquirir novas máquinas e instalações produtivas (Dodig e Hein, 2015). A parcela de receitas financeiras das empresas tem crescido desde o início da década de 1980. A Figura 3 mostra o nível de ativos financeiros como porcentagem dos ativos tangíveis para corporações não financeiras nos EUA. O nível de ativos financeiros mantidos por essas corporações aumentou constantemente em comparação aos ativos tangíveis. A Figura 4 apresenta o nível de "renda financeira" recebida por corporações não financeiras como porcentagem dos recursos internos mantidos pelas empresas. Essas figuras resumem bem a mudança em direção à "gestão financeira" adotada pelas empresas não financeiras desde o final da década de 1970.  

Figura 3 - Ativos financeiros como porcentagem do total de ativos, corporações não financeiras. Estados Unidos.  

Nota: Elaboração própria com base em dados do FRED, 2021.  

2.3. Liberalização Financeira e Consumo Financiado por Dívidas

A crescente disponibilidade de crédito ao consumidor durante a era da financeirização criou condições para o consumo financiado por dívidas. Ao mesmo tempo, o aumento da desigualdade de renda estimulou o consumo por efeito de "gotejamento". De fato, a concentração de renda e riqueza incentivou consumidores de baixa renda a imitar os padrões de consumo dos mais ricos. Essa hipótese da renda relativa (*Relative Income Hypothesis*, RIH) remonta ao trabalho seminal de Duesenberry (1949), que, por sua vez, ecoa a abordagem institucionalista de Veblen (1899). A RIH destaca a importância da formação de hábitos e do comportamento emulativo nos padrões de consumo de diferentes grupos sociais ("manter-se à altura dos vizinhos"). Baseando-se em Duesenberry (1949), Frank, Levine e Dijk (2014) propuseram a chamada hipótese das cascatas de gastos (*expenditure cascades*). Essa hipótese busca explicar a queda na taxa de poupança observada nos EUA durante o período de financeirização por meio de um mecanismo de cascata: gastos mais altos das famílias no quintil (ou decil) superior de renda levam os quintis subsequentes a aumentarem seus gastos. Essa imitação, por sua vez, eleva o consumo das famílias no terceiro quintil mais alto, e assim por diante.  

Figura 4 - Razão entre dividendos e lucros não distribuídos (%), corporações não financeiras. Estados Unidos.  

Nota: Elaboração própria com base em dados do *US Bureau of Economic Analysis* (BEA), 2021.  

Em alguns casos, o boom de consumo financiado por dívidas privadas compensou o impacto contracionista da redistribuição de renda em favor da parcela mais rica da população, bem como o efeito depressivo da queda no investimento líquido das empresas de produção.  

Além disso, novas normas financeiras, instrumentos financeiros e práticas financeiras reduziram os padrões de avaliação de crédito. Essas mudanças — geralmente chamadas de "liberalização financeira" — também incentivaram o aumento do crédito ao setor doméstico. Esse aspecto específico da financeirização é analisado no primeiro experimento da Seção Quatro.  

**2.5. Desenvolvimento Financeiro**  

A distinção entre liberalização financeira e desenvolvimento financeiro foi proposta pela primeira vez por Abiad, Oomes e Ueda (2008). O último inclui tanto a ampliação dos serviços financeiros para novos usuários (margem extensiva) quanto a melhoria da qualidade dos serviços financeiros para usuários antigos (margem intensiva). O desenvolvimento financeiro é frequentemente medido pela relação entre o crédito total (para o setor privado) e o PIB. A Figura 5 mostra o aumento dramático do desenvolvimento financeiro em nível internacional durante a era da financeirização, com períodos de aceleração abrupta em alguns países (no Reino Unido em meados da década de 1980 e na Suécia no final da década de 1990).  

**2.6. Regimes de Crescimento Baseados em Dívidas vs Baseados em Exportações**  

A combinação dos pontos apresentados nas Seções 2.3 (consumo financiado por dívidas) e 2.4 (liberalização da conta de capital) gerou um padrão típico de crescimento frequentemente descrito como regime de boom de demanda privada baseado em dívidas. Em particular, os EUA têm dependido cada vez mais do consumo para sustentar a demanda doméstica. No entanto, isso gerou uma maior demanda por bens estrangeiros, fomentando regimes de crescimento complementares baseados em exportações (como os da Alemanha, Japão e Suécia). Por sua vez, os superávits externos das economias baseadas em exportações foram investidos na dívida dos Estados Unidos e de outros países deficitários, graças à liberalização da conta de capital.  

Figura 5 - Crédito doméstico ao setor privado (% do PIB). Países selecionados da OCDE.  

Nota: Elaboração própria com base em dados do Banco Mundial, 2021.  

Um regime baseado em exportações também pode se originar de dinâmicas fracas de alguns componentes autônomos da demanda agregada, como os gastos governamentais, em vez de ser impulsionado pelo aumento da desigualdade ou do poder crescente das finanças. Ainda assim, os desequilíbrios gerados por esses padrões de crescimento desiguais só podem ser sustentados na presença de algum grau de liberalização financeira e desenvolvimento financeiro, como a história recente da Zona do Euro tem demonstrado.  

No entanto, a relação entre esses diferentes regimes de crescimento é mais complexa do que geralmente se reconhece. Na Seção Quatro, mostramos que, por mais contraintuitivo que possa parecer, o fim de um regime de crescimento baseado em dívidas em um país não tem o mesmo efeito negativo (de longo prazo) sobre seus parceiros comerciais.  

Mudança técnica, taxa de exploração constante e queda na taxa de lucro em economias de produção linear - Basu e Orellana (2022)

Mudança técnica, taxa de exploração constante e queda na taxa de lucro em economias de produção linear - Basu e Orellana (2022)

SUMÁRIO

1 | INTRODUÇÃO

2 | A CONFIGURAÇÃO

2.1 | Configuração inicial

2.1.1 | Taxa uniforme de lucro e preços de produção

2.1.2 | Valores do trabalho e taxa de exploração

2.1.3 | Pacote inicial de salário real

2.2 | Mudança técnica CU-LS viável

2.3 | Luta de classes e um novo pacote de salário real

3 | RESULTADOS

4 | DISCUSSÃO

5 | UM EXEMPLO

5.1 | Situação inicial

5.2 | Mudança técnica CU-LS viável

5.3 | Luta de classes e um novo pacote de salário real

6 | CONCLUSÃO

APÊNDICE A: PROVAS DOS TEOREMAS

A.1 | Prova do Teorema 1

A.2 | Prova do Teorema 2

A.3 | Prova do Teorema 3

RESUMO

Pode a mudança técnica que reduz custos levar a uma queda na taxa de lucro de longo prazo, se a luta de classes conseguir manter constante a taxa de exploração? Neste artigo, derivamos três resultados que, juntos, respondem afirmativamente a essa questão. Primeiro, identificamos três propriedades que novos pacotes de salário real devem satisfazer para manter a taxa de exploração constante e levar a uma queda na taxa de lucro. Em segundo lugar, derivamos condições suficientes para a existência de um número infinito de tais pacotes de salário real. Terceiro, mostramos que, se o pacote inicial de salário real for tal que a razão máxima entre o preço e o valor do trabalho for maior que 1 mais a taxa de exploração, então, partindo de qualquer configuração de tecnologia, sempre existe uma mudança técnica viável, poupadora de trabalho e que utiliza capital, que satisfaz as condições suficientes do resultado anterior. Esses resultados corroboram a afirmação de Marx de que, se a taxa de exploração permanecer inalterada, então a mudança técnica nas economias capitalistas pode levar a uma queda na taxa de lucro de longo prazo.

1 | INTRODUÇÃO

Se a taxa de lucro tem uma tendência a declinar com o desenvolvimento capitalista foi um tema de grande interesse para a economia política clássica. Sendo a fonte de renda da classe capitalista, o lucro é tanto a origem quanto o estímulo para a acumulação de capital. Se houvesse uma tendência de queda contínua na taxa de lucro ao longo do tempo, isso naturalmente indicaria alguma contradição profunda no sistema capitalista. Pois, por meio dessa tendência, o sistema parecia se autossabotar de forma endógena (Dobb, 1945, Capítulo IV).

Adam Smith argumentou que a acumulação de capital e a competição entre capitalistas imprimiriam uma tendência de queda à taxa de lucro. David Ricardo, embora discordando da explicação de Smith, ainda sentiu-se compelido a oferecer sua própria resposta. Os retornos decrescentes sobre a terra, argumentou Ricardo, eram a fonte última da tendência de queda da taxa de lucro. Com a acumulação de capital, há um aumento na demanda por trabalho e, portanto, por alimentos. Isso, por sua vez, exige o cultivo de terras inferiores, elevando o preço do trabalho e comprimindo os lucros (Dobb, 1945, Capítulo IV, pp. 86–87). O argumento de Ricardo deslocou o foco da tendência decrescente da taxa de lucro para fora do capitalismo, para as possibilidades ou não de progresso técnico na produção agrícola. Marx trouxe o foco de volta para a dinâmica interna do capitalismo.

Desenvolvendo seu próprio argumento sobre a lei da queda tendencial da taxa de lucro no Volume III de O Capital, Marx argumentou que o progresso técnico na produção capitalista, que provoca um aumento na composição orgânica do capital (a relação entre os custos materiais e de trabalho), manifestar-se-ia como uma “tendência” de queda na taxa de lucro se o grau de exploração do trabalho pelo capital permanecesse constante (Marx, 1993) [1]. É irrelevante se há ou não progresso técnico na agricultura. Enquanto a composição orgânica do capital tiver uma tendência a crescer no nível agregado, o progresso técnico, a própria força do capitalismo, o minará ao imprimir uma tendência de queda na taxa de lucro.

[1]: “Se agora assumirmos, além disso, que essa mudança gradual na composição do capital não caracteriza apenas certos ramos individuais de produção, mas ocorre mais ou menos em todas as esferas, ou pelo menos nas decisivas, e que, portanto, envolve mudanças na composição orgânica média do capital total pertencente a uma determinada sociedade, então esse crescimento gradual do capital constante, em relação ao variável, deve necessariamente resultar em uma queda gradual na taxa geral de lucro, desde que a taxa de mais-valia, ou o nível de exploração do trabalho pelo capital, permaneça o mesmo.” (Marx, 1993, pp. 317–318, ênfase no original).

A partir de Okishio (1961), uma extensa literatura argumentou que o argumento de Marx é falho. Se os capitalistas adotarem novas técnicas de produção que reduzem o custo de produção aos preços vigentes, o que parece razoável, então a taxa geral de lucro tenderá a subir, e não a cair. Para ser mais preciso, se os produtores capitalistas optarem por adotar uma nova técnica de produção apenas se ela reduzir custos aos preços atuais e a taxa de salário real permanecer inalterada, então a taxa de lucro de longo prazo na economia aumentará (Bowles, 1981; Dietzenbacher, 1989; Okishio, 1961; Roemer, 1977, 1981; Samuelson, 1974). Esse resultado é hoje conhecido como Teorema de Okishio (TO).

O TO baseia-se na suposição de que a taxa de salário real não muda. Essa é uma suposição extremamente restritiva, dado que a análise trata de preços e taxas de lucro de longo prazo. Afinal, o TO compara dois equilíbrios de longo prazo, um antes e outro depois da mudança técnica. Não há razão teórica ou empírica para acreditar que a taxa de salário real permaneça constante ao longo da mudança técnica, isto é, da adoção de uma nova técnica de produção por um capitalista inovador e sua subsequente difusão pelo restante da economia [2]. Na realidade, a mudança técnica interage com forças sociais e econômicas mais amplas, incluindo aquelas relevantes para os resultados do mercado de trabalho, e não é inconcebível que a taxa de salário real possa mudar - de uma forma ou de outra - ao longo da mudança técnica.

[2]: O próprio Okishio (2000) admite que a suposição de uma taxa de salário real constante é irrealista. “A suposição de uma taxa de salário real constante implica ou uma economia não monetária ou a adaptação instantânea da taxa de salário monetário aos preços dos bens de consumo. Ambas são irrealistas. Uma economia capitalista é uma economia de produção monetária. Os trabalhadores recebem um salário em dinheiro. A taxa de salário monetário e os preços dos bens de consumo mudam devido à concorrência no mercado de bens de consumo e no mercado de trabalho. A suposição de uma taxa de salário real constante não pode ser mantida.” (Okishio, 2000, p. 493).

Parece plausível que a taxa de salário real seja resultado da luta de classes ou de negociação entre trabalhadores e capitalistas. Portanto, não está claro por que a luta de classes não poderia alterar a taxa de salário real ao longo da mudança técnica. No mínimo, parece plausível argumentar que, como a mudança técnica aumenta a produtividade do trabalho, os trabalhadores tentarão negociar por uma parte dos ganhos da mudança técnica, especialmente em um contexto de restrições de trabalho (Dobb, 1945, pp. 113–114). Assim, é perfeitamente possível que a taxa de salário real aumente com a mudança técnica, em vez de permanecer inalterada, em economias capitalistas avançadas marcadas por restrições de trabalho. Um achado importante da literatura marxista sobre mudança técnica e lucratividade é que o TO não se sustentará se permitirmos que o salário real mude ao longo da mudança técnica (Basu, 2021; Dietzenbacher, 1989; Foley, 1986; Laibman, 1982, 1992; Liang, 2021; Michl, 1988; Roemer, 1978). Embora esse resultado geral seja bem conhecido, ainda é uma questão em aberto se a afirmação de Marx sobre a tendência de queda da taxa de lucro em equilíbrio pode ser estabelecida. Existem duas abordagens amplas para lidar com essa questão, ambas formalizando a afirmação de que a taxa de salário real muda ao longo da mudança técnica.

A primeira abordagem trabalha com uma razão constante de lucro-salário em nível setorial como uma descrição plausível de como a taxa de salário real pode se comportar ao longo da mudança técnica. A intuição subjacente é que a negociação entre trabalhadores e capitalistas mantém constante a participação dos salários em relação aos lucros em nível setorial (Roemer, 1978, pp. 156) [3]. Em um modelo de dois setores, Roemer (1978, 1981) mostra que a taxa de lucro cai (ou permanece inalterada) se houver mudança técnica poupadora de trabalho e que usa capital (CU-LS) no setor de bens de capital (ou de bens de consumo). Este resultado foi generalizado para o caso de um modelo de n-mercadorias – sem distinguir entre indústrias de bens de capital e de consumo – em Chen (2019), que mostra que, quando há uma mudança técnica CU-LS que reduz custos em qualquer setor, com as razões lucro-salário setoriais permanecendo constantes, a taxa de lucro em equilíbrio cai. Uma desvantagem dessa abordagem é que o salário real deve ser permitido variar entre os setores. Assim, precisamos assumir implicitamente mercados de trabalho não competitivos [4].

[3]: “A teoria que adotaremos é que a negociação entre trabalhadores e capitalistas opera de tal forma a manter uma razão constante entre lucros e salários, antes e depois da mudança técnica. A história simplificada é a seguinte: após a adoção de uma inovação que reduz custos, ... os trabalhadores ou seus sindicatos então avaliam o que aconteceu com sua participação relativa e, se esta diminuiu, lutam por meio de greves, etc., para restabelecer a antiga proporção. Do outro lado, se a participação relativa dos trabalhadores foi aumentada pela mudança técnica, então os sindicatos não serão particularmente vigilantes enquanto os capitalistas diminuem gradualmente o salário real até que a antiga proporção relativa seja restabelecida.” Roemer (1978, pp. 156).

[4]: “[S]erá impossível manter participações relativas constantes em cada setor antes e depois da mudança técnica, e o mesmo salário real em ambos os setores.” (Roemer, 1978, p. 157).

A segunda abordagem usa uma taxa de exploração constante (a razão entre o tempo de trabalho não pago e o tempo de trabalho pago) como uma descrição de como o salário real pode variar ao longo da mudança técnica [5]. A ideia de que a taxa de exploração pode permanecer constante antes e depois da mudança técnica remonta, como vimos acima, a Marx (1993). A intuição subjacente dessa abordagem é que a luta de classes entre trabalhadores e capitalistas consegue manter constante a taxa de mais-valia, ou o grau de exploração do trabalho pelo capital (a razão entre o trabalho pago e não pago) [6]. Laibman (1982, 1992) incorporou essa suposição em um modelo de dois setores e analisou o efeito da mudança técnica sobre a taxa de lucro. A principal descoberta de Laibman (1982) foi que é possível que a taxa de lucro caia após uma mudança técnica que reduz custos se a taxa de exploração permanecer constante. Embora Michl (1988) e Basu (2021, Capítulo 6) apresentem resultados semelhantes em um modelo de um setor, Liang (2021) generalizou o resultado de Laibman para um modelo de dois departamentos com m setores e capital fixo.

[5]: Como a mudança técnica implicará um aumento na produtividade do trabalho, uma taxa de exploração constante implicará algum aumento na taxa de salário real.

[6]: “É a taxa de exploração – a razão entre o tempo de trabalho não pago e o tempo de trabalho pago – que expressa o equilíbrio das forças de classe em um determinado momento. É quando os salários acompanham a produtividade que o equilíbrio das forças de classe não muda; esse é, então, o quadro neutro no qual se pode analisar a mudança técnica.” (Laibman, 1992, p. 122).

A principal contribuição deste artigo é estender os resultados de Laibman (1982), Michl (1988), Basu (2021, Capítulo 6) e Liang (2021). Primeiro, estendemos a análise de Laibman (1982), Michl (1988) e Basu (2021, Capítulo 6) para um modelo geral de capital circulante de n setores em uma economia capitalista com uma tecnologia de produção linear, sem distinguir entre setores de bens de capital e de consumo. Segundo, estendemos a análise em Liang (2021) permitindo uma mudança geral no pacote de salário real. Enquanto Liang (2021) permite apenas mudanças proporcionais no vetor do pacote de salário real, nós permitimos que o pacote de salário real mude de maneira arbitrária ao longo da mudança técnica. Nesse cenário geral, demonstramos que, sob certas condições plausíveis, a taxa de lucro de longo prazo em equilíbrio pode cair após uma mudança técnica que reduz custos se a taxa de exploração permanecer constante (ou até aumentar de forma limitada). Assim, demonstramos que a afirmação de Marx sobre a tendência de queda da taxa de lucro pode ser sustentada em um modelo bastante geral.

O restante do artigo está organizado da seguinte forma. Na Seção 2, descrevemos a configuração básica e definimos mudança técnica CU-LS viável. Na Seção 3, identificamos três propriedades de um novo pacote de salário real que podem manter constante a taxa de exploração e levar a uma queda na taxa de lucro em equilíbrio (Teorema 1); em seguida, derivamos condições suficientes para a existência de um número infinito de tais pacotes de salário real (Teorema 2); finalmente, mostramos que, se impusermos uma restrição menor ao conjunto permitido de pacotes de salário real antes da mudança técnica, então, partindo de qualquer configuração de tecnologia, sempre haverá mudanças técnicas CU-LS viáveis que satisfarão as condições suficientes do Teorema 2 (Teorema 3). Na Seção 4, oferecemos uma intuição e discussão sobre nossos resultados. Na Seção 5, apresentamos um exemplo de um modelo de 3 setores para ilustrar nosso argumento; finalmente, concluímos o artigo na Seção 6. As demonstrações das proposições estão reunidas no Apêndice A.

2 | A CONFIGURAÇÃO

2.1 | Configuração inicial

Para a análise deste artigo, utilizamos um modelo de Leontief/Sraffa, onde a economia é composta por n setores de produção. A tecnologia é dada pela matriz de insumo-produto n × n, não negativa, A ≧ 0, e pelo vetor 1 × n de insumos diretos de trabalho, L ≫ 0. O pacote de salário real, que representa a distribuição, é dado pelo vetor n × 1, b ≧ 0 [7]. Cada setor produz uma mercadoria com uma única técnica de produção, e não há capital fixo [8].

[7]: Para vetores e matrizes, usaremos a seguinte notação: x ≧ 0, se para i = 1, 2, …, n, xi ≥ 0 e x ≠ 0; x ≫ 0, se para i = 1, 2, …, n, xi > 0.

[8]: Na tradição clássica marxista, este é um modelo comumente utilizado para estudar o efeito da mudança técnica na lucratividade; veja, por exemplo, Roemer (1979, Seção 2, pp. 381–383).

Os Problemas da Oferta e Demanda - John Weeks

A Fraude da Oferta e Demanda - John Weeks (Economics of the 1%)

A expressão "oferta e demanda" é usada no discurso cotidiano para transmitir a ideia de que eventos econômicos estão além da influência dos indivíduos, determinados por “forças de mercado”. Por exemplo, em março de 2007, no Farmer’s Guardian (Reino Unido), um artigo invocou a Lei de Oferta e Demanda para “explicar” os preços dos grãos no Reino Unido, deixando os detalhes à imaginação do leitor:

"As razões por trás do aumento de preços [dos grãos] são bem documentadas. A escassez mundial e a suposta demanda crescente da suposta indústria de biocombustíveis estão colocando um verdadeiro piso no mercado de commodities de trigo, à medida que mais compradores entram no mercado. Felizmente, as leis de oferta e demanda que aprendi na minha juventude ainda permanecem verdadeiras."

Encontramos um insight semelhante (de que um preço aumenta quando mais pessoas querem mais de algo) em discussões sobre preços de petróleo. Aqui, parece que é o preço que afeta a demanda, em vez de a demanda afetar o preço:

"A oferta e a demanda continuam entre os componentes mais influentes no comportamento do mercado de petróleo. Diferente de outros mercados, no entanto, mudanças drásticas nos preços do petróleo não necessariamente provocam mudanças na demanda. "Os preços podem cair muito sem estimular a demanda," diz Tim Evans, analista de energia do Citigroup.

Questões de oferta, por outro lado, podem ter impacto considerável nos preços do petróleo. Eventos geopolíticos que ameaçam o suprimento de petróleo, como problemas entre a Venezuela e os Estados Unidos ou entre a Turquia e o Iraque Curdo, podem assustar investidores e levar à volatilidade dos preços."

Na mesma linha incoerente, lemos no Economist: “Dois fatores determinam o preço de um barril de petróleo: as leis fundamentais de oferta e demanda, e o medo puro.” Essas afirmações têm implicações tanto prescritivas quanto ideológicas, sugerindo que os mercados produzem resultados “fundamentais” que estão além do poder de indivíduos, grupos ou governos para alterar e que esses resultados ocorrem desde que as pessoas negociam coisas. Tentativas de interferir nas “leis fundamentais de oferta e demanda” são equivocadas e fadadas ao fracasso.

Para avaliar esse fundamentalismo de mercado, reformulo a essência dessas citações sem usar as palavras “oferta” e “demanda”:

"Quando empresas e pessoas querem comprar mais de algo pelo preço atual, esse preço tende a subir. Se uma empresa não consegue vender todo o seu estoque, ela pode baixar o preço e talvez vender mais. Quanto mais depende das características de cada mercadoria."

Como previsões de comportamento real, essas afirmações podem ou não ser verdadeiras. Por exemplo, em 2011, a exaustão dos estoques de varejo dos dispositivos iPad 2 no Reino Unido não resultou em aumento de preço. Isso ocorreu porque o produtor, Apple, usou seu poder de mercado para manter os preços no varejo constantes. Isso foi uma violação das “leis fundamentais de oferta e demanda” ou prova de sua operação? Ou ambos?

Seja verdadeira ou falsa, as citações acima não têm relação com o que economistas ou econfakers (falsos economistas) entendem por “oferta e demanda”. O “medo puro” pode ou não impactar o preço do petróleo, como especula o Economist. Sem saber medo de quê, é impossível avaliar essa banalidade. Mas nenhum economista competente (e poucos econfakers) sugeriria que “as leis fundamentais de oferta e demanda” determinam o preço de um barril de petróleo, como irei explicar.

A “oferta” de uma mercadoria ou serviço e a “demanda” por ela são construções teóricas. Essas construções teóricas existem apenas no mundo imaginário da concorrência perfeita, um conceito não confiável que já desmontei anteriormente. Aqui, basta explicar que comprar e vender, preços subindo e descendo, e excessos e escassezes de mercadorias não são a operação de qualquer lei econômica, muito menos algo que poderia legitimamente ser chamado de Lei de Oferta e Demanda, ou a “lei” de qualquer coisa.

As mercadorias são produzidas e entregues aos distribuidores atacadistas e varejistas. Pessoas, empresas e governos demonstram quanto querem dessas mercadorias comprando-as dos distribuidores. Nesse sentido simples e cotidiano, as mercadorias têm uma oferta e há uma demanda por elas. As palavras significam nada mais do que “alguém vende” e “alguém compra”. As atividades reais de compra e venda não são a Lei de Oferta e Demanda tornada infame pelos econfakers, e são avidamente deturpadas por ideólogos do livre mercado em veículos populares como o Economist.

A produção, distribuição e troca no mundo real estão sujeitas a manipulação por meio de poder de mercado, tanto por compradores quanto por vendedores. Tomando o exemplo óbvio, os produtores de petróleo não aceitam passivamente os preços. Eles manipulam preços diretamente por meio de acordos colusivos ou indiretamente ajustando o que oferecem para venda. Oferta e demanda não determinam os preços do petróleo. Muito pelo contrário, os preços do petróleo administrados pelo monopólio determinam quanto será comprado, e os produtores de petróleo ajustam sua “oferta” para essa demanda.

Como qualquer iniciante aprende em economia introdutória (mais precisamente, introdução à fakeconomia), a “oferta” na Lei de Oferta e Demanda não significa uma quantidade. A palavra se refere a uma lista de quantidades de uma mercadoria que um produtor ofereceria para venda a diferentes preços. Essas não são vendas reais ou entregas ao varejista. As quantidades na lista ou programação são quantidades planejadas ou antecipadas que poderiam ser oferecidas se vários preços previstos aparecessem no mercado. São quantidades para preços hipotéticos quando o preço real de venda é desconhecido para o vendedor.

Por exemplo, um alfaiate pode planejar produzir e entregar cinco camisas sob medida em uma semana a um preço de $50 cada, oito se o preço subir para $60, e assim por diante. Pode parecer óbvio que um produtor oferecerá mais quando os preços subirem. Essa relação simples prova ser extremamente difícil para os econfakers estabelecerem como uma regra geral, como explicarei.

Essas ofertas e os preços previstos não podem ser observados. Eles são imaginários, às vezes chamados de “oferta notional” no jargão da fakeconomia. Quando os produtores combinam as quantidades imaginárias com preços imaginários, essa combinação possui uma propriedade extremamente importante. O produtor deve acreditar que cada quantidade planejada será vendida integralmente ao preço previsto (isto é, o preço na correspondência quantidade–preço). Formalmente falando, a “oferta” da “oferta e demanda” consiste nas quantidades de cerveja, computadores etc. que cada empresa oferece a cada preço concebível, firme na crença de que as vendas são potencialmente ilimitadas. Mas se as vendas potenciais não têm limite, de onde vêm as quantidades para corresponder aos preços? Por que não “oferecer” até que a alfaiataria opere 24 horas por dia com o máximo de assistentes que o mestre alfaiate puder acomodar? “Ah, aí está o problema,” como Hamlet poderia dizer se fosse economista – um problema muito sério, explorado abaixo.

O leigo pode justificadamente perguntar qual a relação entre essa combinação imaginária de quantidades e preços com a produção e distribuição reais de mercadorias e serviços? A resposta é “nenhuma”. Qualquer CEO ou gerente de vendas que agisse acreditando que tudo o que fosse oferecido seria vendido logo estaria buscando outro emprego, após levar sua empresa à falência. Por mais improvável que a crença na ausência de limite de vendas possa ser, prossigo com essa falta de lógica da fakeconomia até o fim da história, pois ela revela a verdadeira história da oferta e demanda.

Se cada unidade de um item produzido por uma empresa fosse igual, por exemplo, um DVD do Titanic, esperaríamos que cada unidade tivesse o mesmo custo de produção conforme a produção aumentasse. Tentemos combinar essa generalização razoável sobre custos unitários com a ideia improvável de que as empresas decidem suas ofertas acreditando firmemente que não têm limite de vendas.

A combinação de custo unitário constante e vendas ilimitadas implica que a empresa de DVDs em busca de lucros operaria suas máquinas 24 horas por dia, 365 dias por ano, produzindo o máximo possível. Deveríamos observar produtores, desde alfaiates até multinacionais, operando continuamente à capacidade máxima. Mas não observamos isso – muito pelo contrário. A capacidade ociosa se manifesta com frequência, até continuamente. Ou a lógica está incompleta ou está errada.

Como em quase toda generalização da fakeconomia, o que começou como uma ideia aparentemente simples (de que os mercados geram preços determinados pela oferta e demanda do que as pessoas compram e vendem) prova ser extremamente difícil de estabelecer na lógica, muito menos na prática. A solução para o enigma da oferta e demanda exige peças adicionais não antecipadas no início, algumas com formas bastante estranhas. Com demanda ilimitada e custos unitários constantes, haveria apenas dois níveis de produção (oferta). Se o preço de venda estiver abaixo do custo unitário, a empresa terá prejuízos e removerá o produto de sua lista de vendas (oferta zero). Se o preço subir acima do custo unitário, a empresa produzirá na capacidade total.

Qualquer outro nível de produção, entre zero e máximo, significaria que a quantidade produzida e oferecida veio de uma estimativa das vendas previstas da empresa. Embora essa inferência pareça razoável e realista, ela tem um impacto devastador na “lei fundamental da oferta e demanda.” Quando as vendas previstas, e não os preços previstos, determinam a produção, a quantidade prevista demandada dita a quantidade real ofertada – oferta e demanda são a mesma coisa.

Essa tautologia torna a suposta Lei de Oferta e Demanda nada mais do que uma redundância banal. Se os proprietários das empresas acreditam que não têm restrições de vendas, então continuarão expandindo suas instalações de produção até que uma, ou poucas delas, controlem todo o mercado. Nesse ponto, os compradores se tornam receptores passivos dos preços determinados por monopólios poderosos ou “oligopólios” (um vendedor ou poucos vendedores, respectivamente).

Se oferta e demanda determinam os preços, então oferta e demanda devem ser independentes entre si. As tesouras de oferta e demanda precisam ter duas lâminas, não uma. Os compradores (consumidores) determinam a demanda, e os vendedores determinam a oferta. Se custos unitários constantes caracterizam a produção de uma empresa, as vendas previstas determinam a oferta. Oferta e demanda coincidem. A independência da oferta em relação à demanda (vendas previstas) exige que a empresa acredite que a demanda por seu produto seja ilimitada. Se a demanda é ilimitada e os custos unitários são constantes, a oferta é independente da demanda, mas temos apenas dois resultados possíveis: zero e máximo.

Para reiterar o dilema, a famosa Lei de Oferta e Demanda se coloca em uma encruzilhada tautológica. Se, ao preço atual, as vendas são potencialmente ilimitadas, então a produção estará sempre na capacidade máxima. Como resultado, a oferta é uma quantidade única, não afetada pelo preço a menos que ele caia abaixo do custo unitário. Se o preço está acima do custo unitário, os aumentos de preço não impactam a quantidade produzida (oferta); eles afetam apenas o lucro unitário. Se as vendas não são ilimitadas, a quantidade ofertada não é conhecida até que as vendas sejam realizadas. Oferta e demanda são a mesma coisa.

Existe uma rota de escape para evitar essa concentração de mercado, se abandonarmos os custos unitários constantes. Devemos ser cautelosos ao fazer isso, pois um passo em falso fora dos custos constantes pode ter consequências fatais. Considere os casos opostos: custos unitários crescentes e custos unitários decrescentes. Se os custos unitários de uma empresa aumentam continuamente à medida que a produção aumenta, ela não terá muito tempo para operar. Sob pressão da concorrência de preços, os gestores da empresa perceberiam que, para reduzir os custos unitários, precisam diminuir o nível de produção, levando a produção e as vendas para baixo, até o fechamento. O caso oposto é, se possível, ainda pior para a suposta Lei de Oferta e Demanda. Custos unitários continuamente decrescentes levam ao monopólio. Cada empresa aumentará sua escala de operações até que uma delas possa satisfazer todo o mercado. As ferrovias nos EUA durante o século XIX e a primeira metade do século XX forneceram exemplos claros de custos unitários decrescentes, à medida que o enorme investimento fixo se diluía em escalas maiores e maiores de operação. Como resultado, as ferrovias em todos os países do mundo são, ou um monopólio público, ou monopólios privados regulados publicamente.

O que pode salvar a Lei de Oferta e Demanda da tautologia? Custos unitários constantes não conseguem gerar uma curva de oferta significativa, nem custos unitários crescentes ou decrescentes. O processo de eliminação analítica leva a uma solução, embora um tanto absurda. Precisamos de uma explicação plausível de por que os custos unitários poderiam primeiro cair, depois estabilizar e, posteriormente, subir, resultando em um custo unitário em forma de “U”. Se essa sequência improvável pudesse ser justificada e generalizada, daria esperança ao conceito de “oferta”. Uma empresa com custos em forma de “U” teria um custo unitário mínimo entre as porções decrescente e crescente.

Uma história de oferta e demanda poderia ser assim: na crença de que podem vender tudo o que produzem, as empresas ajustam sua produção ao nível de custo que maximiza o lucro para cada preço. À medida que o preço de mercado aumenta, isso compensa os custos unitários crescentes e induz a empresa a oferecer uma quantidade maior para venda. Com o tempo, a concorrência entre os produtores força as empresas a seu ponto de menor custo unitário. Se o nível de produção para cada empresa no custo unitário mínimo contribui com uma pequena fração para as vendas totais ao consumidor, então a indústria pode sustentar muitas empresas.

O mecanismo para evitar o monopólio de um lado e a produção zero do outro foi encontrado, na simples letra “U” aplicada aos custos unitários. Uma dificuldade infeliz permanece. Estruturas de custo unitário em forma de U não existem no mundo real. A “solução” é um passo descaradamente ex machina. Na ausência de um mecanismo conhecido para tal estrutura de custo, os econfakers inventam uma e a repetem infinitamente, como se fosse crível. A criação inventiva é a Lei dos Rendimentos Decrescentes da fakeconomia. Essa nova lei afirma que, se combinarmos mais de um “insumo variável” (isto é, trabalhadores) com um “insumo fixo” (planta e maquinaria, “capital”), a produção aumenta, mas a uma taxa decrescente. Do nada, essa “lei” gera a história da produção em forma de U tão desesperadamente necessária.

Antes de prosseguir, devo enfatizar que essa suposta lei, tirada como um coelho da cartola, não tem parentesco com o conceito de rendimentos decrescentes de David Ricardo do início do século XIX, embora os econfakers o invoquem para dar credibilidade. Em seu famoso trabalho, *Princípios de Economia Política e Tributação* (1817), Ricardo argumentou que a fertilidade da terra em cada país varia. Os agricultores capitalistas plantarão primeiro nas terras mais férteis, que geram o maior lucro, depois nas menos férteis, onde o lucro será menor, o que é o princípio dos “rendimentos decrescentes na margem extensiva”, para usar o jargão.

Historiadores econômicos e sociais demonstraram além de qualquer dúvida que Ricardo estava errado, devido a restrições sociais e culturais na alocação de terras. Mas, pelo menos, a ideia tem alguma credibilidade superficial, coisa que o custo unitário em forma de U não tem (às vezes, dada a dignidade da expressão “rendimentos decrescentes na margem intensiva”). Qualquer pessoa familiarizada com o trabalho de Ricardo deve sentir simpatia por um grande pensador lembrado principalmente por representações grosseiras de duas de suas ideias: rendimentos decrescentes e “vantagem comparativa” (o próximo capítulo confronta este último).

Para voltar à absurdidade em questão, essa abordagem (“Precisamos de custos unitários em forma de U, vamos chamá-lo de Lei dos Rendimentos Decrescentes”) não deve impressionar uma pessoa racional. Como torná-la crível? A Wikipedia tenta:

Um exemplo comum é adicionar mais trabalhadores a um trabalho, como montar um carro em uma linha de fábrica. Em certo ponto, adicionar mais trabalhadores causa problemas como atrapalhar uns aos outros, ou os trabalhadores frequentemente se veem esperando por acesso a uma peça. Em todos esses processos, produzir mais uma unidade de produção por unidade de tempo acabará por custar cada vez mais, devido ao uso cada vez menos eficaz dos insumos. A lei dos rendimentos decrescentes é uma das leis mais famosas de toda a economia. Ela desempenha um papel central na teoria da produção.

As duas últimas frases são verdadeiras. O resto é lixo. Deduzo que o autor da Wikipedia visitou algumas fábricas de carros bem incomuns. Pode até ser que, à medida que mais e mais trabalhadores se espremem em uma fábrica de automóveis, eles comecem a pisar uns nos outros e a atrapalhar as operações em geral. Duvido que algum gerente de fábrica tenha feito essa experiência para comprovar isso. As empresas dimensionam suas fábricas com base em taxas de equipamentos para trabalhadores tecnicamente determinadas, em fazendas, escritórios e outros locais de trabalho.

A famosa Lei dos Rendimentos Decrescentes sofre de uma nomeação equivocada, pois “rendimentos decrescentes” não geram a forma em U necessária para os custos. Essa forma mágica exige que os “rendimentos” primeiro aumentem (a parte decrescente ou inicial do “U”), depois comecem a diminuir ou “decrescer” (a parte crescente ou final do “U”). Apenas “rendimentos decrescentes” deixam a empresa em um caso fatal de custos continuamente crescentes, discutido acima. A Lei dos Rendimentos Crescentes-seguida-de-Decrescentes é imaginária, um aparato de Rube Goldberg para a “Lei da Oferta” de Heath Robinson.

A Lei de Oferta e Demanda que supostamente determina os preços de mercado não existe, exceto nas imaginações febris dos econfakers. A parte da “oferta” não pode ser especificada logicamente nem verificada empiricamente. Se as empresas acreditassem não ter restrições de vendas, estariam sempre operando a plena capacidade. Se estimam suas restrições de vendas, então a quantidade oferecida e vendida são as mesmas. A solução para esse dilema é a fraude dos Rendimentos Decrescentes. A infame oferta e demanda só são relevantes em um caso muito especial e absurdo, quando os custos unitários de produção de uma empresa apresentam uma forma em U conforme a produção cresce. Um pouco de bom senso, sem viés ideológico, revela como bobagem toda essa complicação sobre oferta e demanda, uma obstrução desnecessária para entender como as empresas tomam decisões e como os mercados operam.

Algo semelhante a “leis” econômicas existe, mas elas estão profundamente enraizadas nas instituições da sociedade, as quais trato no último capítulo. Os custos e preços de mercadorias e serviços não são arbitrários. Eles têm restrições objetivas. A quantidade de bens e serviços que as pessoas e empresas compram e vendem não é arbitrária. Mas encarar a produção e distribuição de forma simplista, como exclusivamente econômicas e determinadas por forças naturais fora do controle das pessoas e de suas ações coletivas, advém da metafísica da fakeconomia, não de um pensamento sólido. Não sou o primeiro economista a apontar isso: “Se a distribuição de riqueza que o funcionamento automático do sistema gera é aceita [sem críticas], o comportamento que interfere na ajuste dos preços relativos é disfuncional… e pode ser condenado em termos éticos. Economistas acadêmicos foram os sumos sacerdotes dessa ética.”

Para a maioria das pessoas, e certamente para todos os econfakers, o nome Karl Marx provoca imagens sombrias de socialismo e comunismo. Seja isso como for ideologicamente, Marx fornece uma visão importante sobre a falsidade da adoração à “oferta e demanda.” Usando o termo “economia vulgar” para o que chamo de fakeconomia, Marx escreveu que ela “se limita a sistematizar de forma pedante e a proclamar como verdades eternas as ideias banais sustentadas por uma burguesia autocomplacente em relação ao seu próprio mundo, para eles o melhor de todos os mundos.”

Substitua “burguesia” por “1%” e vemos o quão pouco mudou na fakeconomia ao longo de 150 anos.

A Taxa de Lucro como uma Taxa Real - Anwar Shaikh (2016)

Medição do Lucro e do Capital - Anwar Shaikh

VIII. MEDIÇÃO DO LUCRO E DO CAPITAL

1. A medição empírica do lucro e do capital é tão complicada quanto a teoria correspondente, mas por razões diferentes. A discussão neste capítulo estabeleceu que o lucro econômico geral é a diferença entre o valor monetário do produto total e o custo corrente de materiais, depreciação e trabalho (seção III.3). Como estabelecido no apêndice 4.1 do capítulo 4, essa quantidade é conhecida nas contas nacionais como Excedente Operacional Líquido (EOL). Um corolário dessa contabilidade é que a medida correspondente do estoque de capital é o custo corrente do capital, não o seu custo histórico. A taxa econômica de lucro é então a razão entre o lucro econômico corrente e o custo corrente do capital adiantado. Calculada dessa maneira, é também uma taxa real de lucro porque calcular o numerador e o denominador em termos de preços correntes ajusta automaticamente para a inflação. Essa propriedade é preservada se desinflacionarmos tanto o numerador quanto o denominador pelo mesmo índice de preços; por exemplo, se desinflacionarmos o custo corrente do capital pelo índice de preços dos bens de capital para derivar o estoque real de capital, então devemos desinflacionar o lucro corrente pelo mesmo índice de preços para obter o lucro real expresso em termos de seu poder de compra sobre bens de capital (apêndice 6.2).

2. A construção do estoque de capital de plantas e equipamentos (inventários serão abordados em breve) apresenta novos desafios decorrentes das dificuldades e armadilhas do método de inventário perpétuo (PIM) através do qual os fluxos de investimento em equipamentos e estruturas são acumulados em estoques de capital [19] (apêndices 6.5.I–II). Precisamos considerar o significado e o impacto dos "ajustes de qualidade" nos índices de preços e quantidades e as importantes implicações para a medição da mudança técnica. É importante perceber que, desde que os ajustes de qualidade foram aplicados às medidas do estoque de capital, a razão ajustada pela qualidade entre a produção real e o capital real deixou de ser um índice da tendência da mudança tecnológica. Isso ocorre porque o propósito oficial dos ajustes de qualidade é fazer com que a quantidade de capital "real" seja proporcional ao lucro "real", sendo este último a qualidade essencial do capital. Na prática, o valor agregado real tende a substituir o lucro real, de modo que o ajuste de qualidade tende a tornar a razão produção real/estoque real estacionária. E como todas as revisões metodológicas são, naturalmente, retomadas até onde os dados permitem, as contas publicadas desde meados da década de 1980 apresentam tendências muito diferentes das publicadas posteriormente (apêndice 6.5.III–V). Interpretar essa mudança como representativa de um “novo estágio do capitalismo” seria um erro grosseiro. Isso nos leva aos aparentemente intratáveis problemas de agregação decorrentes do uso de índices encadeados. Medidas oficiais de estoque de capital são tipicamente calculadas em níveis muito detalhados e depois agregadas em subcategorias. A metodologia anterior utilizava índices de pesos fixos, caso em que os agregados seguem as mesmas regras do PIM que as medidas individuais. Então, poderia-se gerar medidas agregadas alternativas ao alterar uma das suposições subjacentes. Uma vez que a metodologia moderna é baseada em medidas com índices correntes cujos agregados resultantes não obedecem mais às regras do PIM, parece impossível criar medidas alternativas. Por exemplo, uma suposição crucial na metodologia oficial é que a taxa de depreciação de um determinado tipo de bem de capital é imune a eventos econômicos como ciclos de negócios, choques de petróleo e até mesmo Grandes Depressões (incluindo, claro, a atual “Grande Recessão”). No entanto, é bem conhecido que os ciclos econômicos afetam o descarte de plantas e equipamentos, e é até possível estimar o impacto de tais eventos na vida útil média do estoque agregado de capital. Mas, como todas as medidas modernas de estoque de capital dependem de índices ponderados correntes, não parece possível incorporar tais informações no cálculo de novas medidas agregadas. O nó górdio pode ser desfeito ao fazer uma pergunta diferente: mesmo que as medidas agregadas ponderadas correntes não sigam a regra do PIM, há alguma outra regra que elas seguem? Mostro que é possível derivar um novo conjunto de regras generalizadas do PIM que os estoques agregados de capital ponderados correntes seguem, que podem então ser utilizados para fornecer medidas corrigidas do estoque de capital e, portanto, da taxa de lucro (apêndice 6.5.V).

[19]: O Método de Inventário Perpétuo (PIM) é utilizado para construir medidas reais de estoque de capital (KR) a partir dos fluxos brutos de investimento disponíveis (IGR) e da depreciação real estimada (ZR, que é os retiros no cálculo dos estoques brutos e a depreciação no cálculo dos estoques líquidos) de acordo com a regra KRt = (IGRt – Zt) + KRt–1. Na metodologia antiga de pesos fixos, estoques de cada bem de capital individual e o estoque real agregado obedecem a essa regra, então novas medidas agregadas podem ser estimadas fazendo suposições diferentes sobre depreciação. Mas nas medidas ponderadas correntes, enquanto estoques de bens de capital individuais são gerados por essa regra, o agregado resultante pode se desviar muito dessa (Whelan 2000, 16). Veja o apêndice 6.5.V para mais detalhes.

3. A utilização da capacidade apresenta um conjunto adicional de desafios teóricos porque sabemos que a utilização real da capacidade geralmente oscilará em torno de um nível normal. Eu mostro que é possível gerar novas medidas de capacidade e, portanto, de utilização da capacidade, tratando a capacidade real como aquele componente da produção real que é gerado pelos movimentos do estoque de capital real e pela mudança técnica ao longo do tempo. Colocado dessa forma, a capacidade está co-integrada com o estoque de capital sujeito a uma tendência temporal que representa o caminho da razão capacidade-capital (apêndice 6.6). É de particular importância o fato de que a produção e o capital devem ser medidos nas mesmas unidades, de modo que a produção real e o capital real devem ser derivados pela deflação das respectivas medidas de preços correntes por algum índice de preços comum. O índice de preços do estoque de capital é o deflator apropriado no caso clássico porque, então, a produção real representa o poder de compra sobre bens de capital e a razão da produção real assim definida para o estoque real de capital representa a taxa máxima de lucro (apêndice 6.2.II). A estimativa derivada da capacidade permite-nos construir uma medida da utilização da capacidade (a razão entre produção real e capacidade real). A taxa de lucro pode então ser decomposta em dois componentes: um estrutural que representa a taxa normal de lucro obtida na utilização normal da capacidade; e um cíclico que resulta das flutuações da produção real em torno da capacidade produtiva (ou seja, da utilização real em torno do nível normal). É a taxa de lucro normal que é o foco das teorias da tendência de longo prazo da taxa de lucro a cair em Smith, Ricardo, Mill, Marx, Walras, Jevons, Clark, Keynes e Schumpeter, entre outros (Dobb 1973, 52, 72, 89, 157–158; Tsoulfidis 2010, 37–40, 118–120, 191, 252–256). O componente cíclico, por outro lado, é uma preocupação central nas teorias dos ciclos econômicos. Ao ajustar as flutuações devido à capacidade produtiva, conseguimos avaliar o efeito da mudança técnica na relação entre capacidade e produção (a taxa de lucro máxima normal em custo corrente). Por exemplo, a mudança técnica neutra em relação ao capital implica uma relação capacidade-capital estacionária, enquanto a mudança técnica tendenciosa ao capital implica uma relação em queda (Michl 2002, 278). Esta última é fortemente evidente nos dados pós-guerra dos EUA. Os determinantes teóricos da mudança técnica são abordados no capítulo 7, seção VII.

4. Medidas empíricas de lucro e capital vêm a seguir (apêndice 6.7). O primeiro passo para medir o lucro é distinguir dentro das Contas Nacionais de Renda e Produto (NIPA) entre o setor doméstico lucrativo e o governo, negócios sem fins lucrativos e um setor fictício chamado moradia ocupada pelo proprietário (OOH) no qual os proprietários são tratados como empresas alugando suas casas para si mesmos (apêndice 6.7.I.1). Em seguida, precisamos corrigir o fato de que nas NIPA toda a renda das empresas não incorporadas é tratada como parte de seu excedente operacional, em vez de ser dividida entre o equivalente salarial dos proprietários e parceiros e seu lucro efetivo (apêndice 6.7.I.2). Uma vez corrigido esse descuido, as taxas de lucro corporativo e não corporativo acabam sendo muito semelhantes (figura 6.1). Isso significa que podemos usar a taxa de lucro corporativo, que é mais simples de calcular, uma vez que não requer um equivalente salarial como proxy para a taxa geral de lucro.

5. O passo final no lado do lucro é corrigir a presença de encargos de juros imputados fictícios nas contas nacionais. Esta não é uma tarefa simples porque a estrutura dessas imputações é complexa. Nas contas clássicas, e de fato em algumas contas nacionais, os pagamentos líquidos de juros aos bancos são tratados como transferências da renda líquida das famílias e empresas. Mas as NIPA insistem em tratar os bancos como produtores de “serviços bancários,” então acabam adicionando várias quantidades imputadas de juros nas contas de famílias, empresas não financeiras e bancos. As imputações são construídas de forma a deixar as medidas de lucro das NIPA (que são líquidas de juros líquidos reais pagos) inalteradas, mas elas afetam as medidas de valor agregado e excedente operacional. Remover as quantidades imputadas faz com que o excedente operacional líquido volte a ser a soma dos juros monetários líquidos reais pagos e do lucro da NIPA, assim como nas contas clássicas e empresariais. Isso tem um impacto mínimo nas medidas de valor agregado das empresas (aumentando-as em cerca de 1%–2% em 2009) mas um impacto mais substancial nas medidas correspondentes de excedente operacional (aumentando-as em cerca de 10% em 2009). Tomada isoladamente, a correção dos juros imputados aumenta a participação da medida de excedente operacional líquido (NOS) no valor agregado sem afetar substancialmente a razão produção-capital. Este é o único efeito para o setor corporativo, mas no setor não corporativo o ajuste de equivalente salarial discutido anteriormente desloca o equivalente salarial estimado dos proprietários e parceiros para a folha de pagamento e reduz o excedente medido muito mais, de modo que o efeito combinado de ambas as correções é reduzir o excedente operacional total das empresas em cerca de 30% em 2009. Mais uma vez, o setor corporativo é um foco particularmente útil porque o único ajuste necessário para os juros imputados é facilmente feito (apêndice 6.7. IV e tabela do apêndice 6.7.11).

Figura 6.1 - Taxas de Lucro Corporativo e Não-Corporativo

6. No lado do capital, precisamos medir o estoque total (ou seja, a planta, equipamentos e estoques [FB: de bens e produtos que a empresa mantém]). Nas contas nacionais, os dados sobre esses elementos estão disponíveis apenas para empresas domésticas (ou seja, aquelas que operam dentro do país, sejam de propriedade nacional ou estrangeira). Por isso, as medidas correspondentes de VA, NOS e lucro nas seções anteriores focaram em empresas domésticas. Uma vez que quaisquer novas estimativas de estoque de capital indexado por cadeia devem ser feitas através da regra do Inventário Perpétuo Generalizado (GPIM), o primeiro passo é demonstrar que essa técnica de aproximação é 99,5% precisa na geração de proxies para agregados de estoque de capital existentes (apêndice 6.7.V.1). Com o GPIM em mãos, podemos avaliar os efeitos de diferentes pontos de partida iniciais (1925) e diferentes regras de depreciação e desativação sobre medidas alternativas de estoque de capital (apêndice 6.7.V.2–3). A regra GPIM também nos permite ajustar o estoque de capital corporativo para os efeitos da Grande Depressão nas taxas de desativação, efeito estimado através de dados do IRS sobre balanços patrimoniais corporativos. Corrigir apenas esse efeito faz com que o capital fixo a custo corrente comece 28% abaixo da medida oficial do BEA em 1947, mas acaba seguindo mais ou menos o mesmo caminho até 1977 (apêndice 6.7.V.4 e tabela do apêndice 6.8.II.4). Combinar o efeito da Grande Depressão com as medidas anteriormente derivadas de desativação e depreciação então resulta em estimativas finais dos estoques brutos e líquidos de capital fixo (planta e equipamentos). Em comparação com o estoque de capital fixo líquido oficial do BEA (KNCcorpbea), a nova medida de estoque líquido (KNCcorp) começa mais baixa em 1947, mas depois reduz a diferença porque cresce mais rápido. A nova medida de estoque bruto (KGCcorp) começa mais alta do que o estoque líquido oficial do BEA, mas também cresce mais rapidamente do que a medida oficial (apêndice 6.7.V.5).

7. O passo restante no lado do estoque de capital é estimar os inventários corporativos. As NIPA têm dados de setor sobre indústrias privadas (tabela NIPA 5.8.5), mas não por forma jurídica. O Federal Reserve Board (FRB) Flow of Funds tem dados a custo corrente sobre inventários corporativos e estoque de capital, mas apenas para corporações não financeiras [20]. No entanto, o IRS publica balanços patrimoniais corporativos a partir de 1926 e esses contêm dados sobre inventários, e de 1990 a 2011, há dados sobre o estoque de capital histórico líquido. Como os dados do IRS são baseados em amostras, não podemos aplicá-los diretamente ao setor corporativo das NIPA. Devemos, portanto, proceder em duas etapas: primeiro, estimar a razão entre inventários e capital fixo a custo histórico para todo o período de 1947 a 2011; em segundo lugar, escalar os níveis implícitos de inventário para os dos estoques de capital corrigidos no apêndice 6.7.V.5 multiplicando o inventário anterior pela razão entre o capital fixo histórico ajustado e o capital fixo a custo corrente. Como os inventários do IRS são uma mistura de avaliações a custo histórico (FIFO) e a custo corrente (LIFO), adicioná-los ao capital fixo a custo corrente, que é o objetivo, envolve algum grau de erro de avaliação. No entanto, como a rotatividade de inventários é bastante rápida em comparação com a do capital fixo, em comparação com este último, até mesmo os elementos FIFO mais antigos dos inventários são avaliados a preços relativamente recentes, de modo que o estoque agregado de inventário pode ser tratado como sendo bastante atual (apêndice 6.7.V.6).

[20]: Inventários não financeiros a custo corrente excluindo IVA, nome da série = FL105015205.A; capital fixo = equipamentos a custo corrente (FL105020015.A) + estruturas residenciais a custo corrente (FL105012665.A) + estruturas não residenciais a custo corrente (FL105013665.A).

8. O resultado final dessas peregrinações é uma medida expandida de lucro (excedente operacional líquido, ou seja, lucro NIPA mais juros monetários líquidos reais e transferências) e uma medida expandida de capital (capital fixo mais inventários). A medida expandida de lucro líquido é independente da forma como o total é distribuído entre empresas e seus credores, e corresponde à medida contábil empresarial chamada de receita operacional ou Lucro Antes dos Juros e Impostos (EBIT) (Brigham e Houston 1998, 76; Mead, Moulton e Petrick 2004, 3–4). É a medida de lucro apropriada tanto para as abordagens clássica quanto para a keynesiana, pois suas teorias de investimento se baseiam na diferença entre a taxa de lucro e a taxa de juros (capítulos 13 e 16), o que exige que o primeiro seja definido antes dos pagamentos reais de juros. Em contraste, os lucros NIPA são líquidos dos pagamentos reais de juros e transferências. Assim, as empresas com maiores pagamentos líquidos de juros parecerão menos lucrativas e sua rentabilidade parecerá estar em declínio se o componente de encargos de juros se tornar relativamente maior — como foi o caso a partir da década de 1970 (figura 6.2). Os lucros NIPA são semelhantes em espírito aos "lucros líquidos" das empresas, embora os dois possam diferir substancialmente no curto prazo porque o primeiro reflete conceitos de contabilidade econômica nacional, enquanto o segundo reflete conceitos de contabilidade financeira (Hodge 2011).

9. As equações (6.8)–(6.10) delineiam as relações contábeis básicas envolvidas nas medidas corporativas corrigidas. Seja VA = valor adicionado, NOS = excedente operacional líquido, P = lucro NIPA, NMINT = juros monetários líquidos pagos, EC = compensação dos empregados, KGC = capital fixo corrente bruto (estoque de planta e equipamentos), INV = inventários, KTC = KGC + INV = estoque total de capital, R = a taxa máxima de lucro, σP = a participação do lucro expandido (NOS) no valor adicionado, e r = a taxa média de lucro. Então, está claro que a participação do NOS no valor adicionado é o dual da participação correspondente da compensação dos empregados (equação (6.9)), enquanto a participação do lucro NIPA também depende do “peso” dos pagamentos líquidos de juros.

10. A Figura 6.2 exibe novas medidas de rentabilidade corporativa com o valor adicionado e o lucro ajustados para juros imputados e com os inventários incluídos no estoque de capital, juntamente com as medidas correspondentes da NIPA. No topo do gráfico, vemos que a taxa de lucro máxima corrigida (valor adicionado sobre o estoque total de capital) cai mais e de forma mais constante do que a medida da NIPA. Dado que a correção para juros imputados tem apenas um pequeno efeito sobre o valor adicionado (menos de 2%), e considerando que a razão entre inventários e o estoque de capital é bastante estável, essa diferença se deve principalmente às novas medidas de capital fixo bruto (apêndice 6.8.II.5). No meio do gráfico, vemos que a participação do lucro corporativo corrigido (NOS) é maior do que sua contraparte na NIPA porque o ajuste de juros imputados tem um impacto maior sobre o excedente operacional líquido (aumentando-o em cerca de 10%) do que sobre o valor adicionado. Também encontramos que a medida corrigida é muito mais estável, caindo modestamente na “era dourada” do trabalho até o início dos anos 1980, e depois subindo modestamente a partir de então devido ao início das políticas neoliberais. Por outro lado, como o lucro NIPA é líquido dos juros, a queda na participação do lucro NIPA pela metade de meados dos anos 1960 até o início dos anos 1980 deve-se em grande parte à maior participação do NOS absorvida pelos juros líquidos à medida que as taxas de juros aumentam dramaticamente de 3% para 14%, enquanto o aumento na participação do lucro NIPA após os anos 1980 deve-se à queda na participação dos juros líquidos no NOS, pois os crescentes encargos da dívida nesse período são mais do que compensados pela queda dramática na taxa de juros de 14% para perto de zero (capítulo 16, figura 16.6). Veremos no capítulo 16 que a participação dos salários também cai nesse último período, o que aumenta a participação do NOS (σP = profshcorp) um pouco e contribui ainda mais para elevar a participação do lucro NIPA (profshcorpnipa). Finalmente, tanto as taxas de lucro corrigidas quanto as da NIPA caem substancialmente de 1974 a 1982. A taxa corrigida se estabiliza a partir de então porque uma queda na participação dos salários eleva a participação do NOS (6.9), enquanto a taxa da NIPA sobe um pouco devido aos efeitos discutidos anteriormente da queda nas taxas de juros sobre a participação convencional no lucro.

Figura 6.2 - Medidas de Rentabilidade Corporativa Corrigidas para Juros Imputados e Inventários versus Medidas Convencionais da NIPA

11. As diferenças entre as medidas corrigidas e as convencionais giram em torno de três fatores: (1) a derivação de uma nova medida de capital fixo bruto (KGC); (2) a inclusão de juros líquidos pagos (NMINT) no lucro total; e (3) a inclusão de inventários (INV) no capital total. Seja rNIPA = P/KNCnipa a taxa de lucro da NIPA. Então, a taxa de lucro corrigida (r) está relacionada à taxa da NIPA por três variáveis x1, x2 e x3 que representam, respectivamente, as razões de juros monetários líquidos, inventário e estoque de capital.

12. A Figura 6.3 mostra os gráficos de cada uma das razões componentes. A razão de juros monetários x1 aumenta acentuadamente na primeira metade do período à medida que as taxas de juros sobem, e depois se estabiliza à medida que o aumento das dívidas é compensado pela queda acentuada das taxas de juros. A razão de inventário x2 é bastante estável, de modo que os movimentos de x1/x2 são dominados pelos da razão de juros. Por outro lado, como a nova medida de estoque de capital sobe em relação à medida convencional da BEA, x3 diminui constantemente. Assim, (x1/x2) x3, que é a razão da nova taxa de lucro em relação à convencional, apresenta uma tendência de queda com flutuações derivadas dos efeitos dos fluxos líquidos de juros sobre o lucro da NIPA (P = NOS − NMIN).

Figura 6.3 - Razões Componentes que Explicam a Diferença entre as Taxas de Lucro Corrigidas e Convencionais

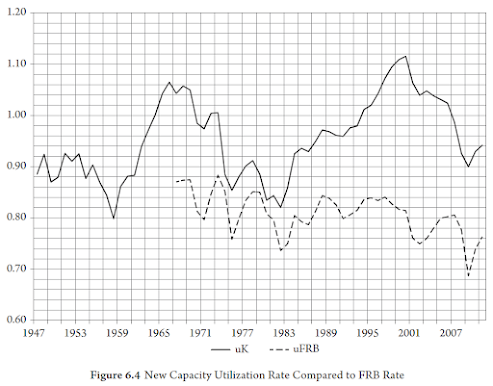
13. As medidas reais de rentabilidade exibidas na Figura 6.2 são um composto de flutuações de curto prazo e padrões estruturais de longo prazo obtidos com a utilização normal da capacidade. Assim, a Figura 6.4 exibe a nova medida de utilização da capacidade ao lado da medida do Federal Reserve Board (FB), esta última disponível apenas a partir de 1967 (apêndices 6.7.VI e 6.8.II.7). A ideia intuitiva por trás das novas medidas é que a capacidade econômica pode ser tratada como aquele aspecto da produção que é co-integrado com o estoque de capital ao longo do tempo, sujeito a uma tendência temporal desconhecida na razão capital-capacidade, cuja magnitude e direção são estimadas a partir dos dados. A nova medida mostra não apenas flutuações de curto prazo, mas também duas flutuações distintas de vinte e cinco anos.

14.A taxa de lucro pode ser decomposta em fatores estruturais e cíclicos. Seja Yn a produção líquida de capacidade normal, uK = Y / Yn = a taxa de utilização da capacidade, cujo nível normal é 1, Rn = (Yn / K) a razão capacidade-capital, que é a taxa máxima estrutural de lucro no sentido de Sraffa, e σPn = (P / Y)n = a participação no lucro normal (ou seja, seu componente estrutural). Com isso em mente, podemos escrever a taxa de lucro real e as taxas de lucro normais da seguinte forma:

15. A Figura 6.5 exibe as taxas máximas e médias corrigidas ajustadas pela nova medida de utilização da capacidade, juntamente com as medidas NIPA/BEA correspondentes ajustadas pela taxa de utilização da capacidade do FRB. A taxa normal máxima de lucro cai de forma constante, apoiando fortemente a noção de que a mudança técnica reduz continuamente a razão produção-capital: em termos neoclássicos, reduz a produtividade média do capital; em termos marxistas, aumenta o equivalente monetário da razão entre o capital constante e o trabalho vivo (Shaikh 1987a); e em termos sraffianos, reduz a taxa máxima de lucro (Sraffa 1960, 16–17). A participação normal no lucro, que é a versão suavizada da participação corrigida no lucro exibida anteriormente na figura 6.2, cai modestamente na chamada Idade de Ouro para o trabalho e, em seguida, compensa totalmente o terreno perdido na era neoliberal subsequente. A taxa média normal de lucro, que é o produto das duas medidas anteriores, cai um pouco mais rápido do que a taxa máxima normal até meados da década de 1980, após o que eventualmente se estabiliza à medida que a participação do salário é substancialmente reduzida diante dos ataques bem-sucedidos ao trabalho e às instituições associadas (capítulo 14, seção II; capítulo 16, seções II.2–3). Pode-se dizer que esse era o objetivo de tais ações, como veremos nos capítulos 14 e 16. As medidas NIPA convencionais se comportam de forma bastante diferente: como a taxa de utilização da capacidade do FRB só está disponível a partir de 1967, só podemos dizer que a máxima normal caiu de 1967 a 1982 e, em seguida, estabilizou-se. A participação normal no lucro da NIPA cai acentuadamente de meados da década de 1960 até o início da década de 1980 devido a uma combinação de aumento na participação dos salários e uma maior proporção do excedente operacional líquido absorvido pelos pagamentos de juros líquidos. Assim, a taxa de lucro ajustada pela capacidade da NIPA cai de 1967 a 1982 rapidamente devido aos efeitos combinados da queda da taxa máxima e da taxa de lucro convencional, apenas para recuperar-se acentuadamente na era subsequente. A Tabela 6.22 resume esses padrões para 1947–82 e a subsequente era neoliberal de 1982–2011. Lembre-se de que as medidas convencionais são construções baseadas em conceitos neoclássicos de estoque de capital e juros imputados (apêndice 6.7). Elas não correspondem ao que as empresas experienciam. Pelo contrário, as medidas corrigidas correspondem mais de perto às reais condições das empresas.

Figura 6.4 - Nova Taxa de Utilização da Capacidade Comparada com a Taxa do FRB

Figura 6.5 - Taxas de Lucro Corporativo com Capacidade Normal, Medidas Corrigidas versus Convencionais

Tabela 6.23 - Decomposição das Taxas Médias de Variação das Taxas de Lucro Corporativo dos EUA e Componentes

Figura 6.6 - Proxies para Taxas de Lucro Corporativo com Capacidade Normal

16. As diferenças finais entre as novas medidas de taxa de lucro e as convencionais podem ser divididas nas influências de dois conjuntos de variáveis: novas medidas de estoque de capital e de utilização da capacidade que afetam a tendência e a suavidade das taxas de lucro; e ajustes de juros imputados e inventários, cuja razão afeta as flutuações, mas não tanto a tendência (figura 6.3). O primeiro conjunto pode sempre ser construído mesmo no nível da indústria sempre que tivermos informações sobre estoque de capital e produção, o que geralmente é o caso para dados de indústria, agregados da OCDE e dados setoriais. O segundo conjunto é frequentemente indisponível em comparações internacionais (como o Banco de Dados Intersetorial da OCDE) e em contas setoriais por indústria (como o PIB por Indústria da BEA [21]). A Figura 6.6 mostra que o primeiro conjunto de variáveis é o mais importante: Rcorpn e rcorpn representam medidas corrigidas por ambos os conjuntos de variáveis, enquanto Rcorp'n e rcorp'n representam aquelas corrigidas apenas pelo primeiro conjunto. As medidas corrigidas e as proxies são bastante similares, o que indica que as correções de estoque de capital e de utilização da capacidade são cruciais para análises de longo prazo.

[21]: http://www.bea.gov/industry/index.htm#annual.

17. Algumas lições gerais podem ser extraídas. Para a análise das tendências nacionais nas taxas de lucro, devemos trabalhar com pelo menos medidas corrigidas de estoque de capital e de utilização da capacidade (capítulo 16). Para comparações interindustriais, essas medidas podem não ser tão importantes na medida em que todas as indústrias compartilham tendências nacionais comuns (capítulos 7 e 9). Isso deixa uma última questão: como esses fatores afetam a taxa sobre o novo capital (investimento), em vez de sobre o capital médio? Dado que a equalização das taxas de lucro entre indústrias é efetuada pela mobilidade interindustrial de capital, o que importa não é a taxa de lucro sobre o capital médio, que engloba tanto capitais obsoletos quanto de ponta, mas sim a taxa de retorno sobre os novos capitais.

18. Argumentarei no capítulo 7, seção VI.5, que a taxa de lucro sobre o novo capital pode ser bem aproximada pela taxa de retorno incremental sobre o investimento, definida como a razão entre a variação no excedente operacional líquido bruto e o investimento bruto atual em capital fixo e inventários [22]. O numerador pode ser calculado adicionando a variação na depreciação por custo corrente à variação no excedente operacional líquido ajustado por imputações calculado anteriormente, e o denominador pode ser calculado adicionando as variações estimadas nos inventários aos dados da BEA sobre investimento bruto em capital fixo. Mas surge uma questão adicional. Como mencionado anteriormente, se a taxa de lucro média é calculada em termos correntes (ou seja, como lucros a custo corrente ajustados para considerar o efeito dos preços correntes sobre a depreciação e os inventários divididos pelo estoque de capital a custo corrente), então é uma taxa real que já reflete os preços correntes (tabela 6.7 e apêndice 6.2). Da mesma forma, se pudéssemos medir diretamente o lucro corrente sobre os novos capitais e seu valor de capital corrente, então a sua razão, que é a taxa de lucro sobre os novos capitais, também seria uma taxa real. Mas a taxa de lucro incremental usada como proxy é diferente porque uma mudança no nível de preços correntes afetaria a mudança nominal no lucro bruto no numerador e o equivalente a custo corrente do investimento bruto no denominador. Portanto, para tornar a taxa de lucro incremental comparável à taxa de lucro média e à taxa de lucro (não observada) sobre o novo capital, devemos expressar seu elemento em termos correntes. Por isso, me referirei a ela como a taxa de lucro incremental corrente, com a compreensão de que é numericamente equivalente a uma taxa real convencional: converter todas as variáveis para preços do ano corrente dá o mesmo resultado numérico que convertê-las para preços do ano base porque os elementos correspondentes em dois cálculos diferem apenas por uma constante que se cancela em sua razão (capítulo 7, seção VI.5).

[22]: Como a taxa de lucro incremental é aproximada pela mudança nos lucros sobre investimentos passados, todas as variáveis devem ser colocadas em unidades de moeda corrente, o que exige que os fluxos do período passado sejam traduzidos em equivalentes do período corrente. Isso é o mesmo que traduzir todos os fluxos para equivalentes do período base (ou seja, em termos reais usando algum índice de preços comum) (capítulo 7, seção VI.5).

19. O cálculo da taxa de lucro incremental de forma a torná-la corrente é diferente da correção neoclássica da taxa de juros para torná-la real. Veremos no capítulo 10 que a equalização das taxas de lucro entre os setores real e financeiro implica que, para qualquer taxa de lucro dada (que por si mesma varia ao longo do tempo), a taxa monetária de juros será proporcional ao nível de preços. A correspondência real entre a taxa de juros monetária e o nível de preços tem sido tão bem documentada (capítulo 10, figura 10.6) que Keynes (1976, 2:198) foi levado a chamá-la de “um dos fatos empíricos mais completamente estabelecidos” na economia. Por outro lado, a economia neoclássica hipotetiza que a taxa de juros está atrelada à taxa esperada de mudança dos preços (taxa de inflação esperada) para qualquer taxa de lucro dada. Sob expectativas racionais, as taxas de inflação esperada e real são estocasticamente iguais, e sob a hipótese do mercado eficiente, a taxa de lucro esperada é constante ao longo do tempo, então acabamos com a hipótese clássica de que a taxa de juros (i) espelha a taxa real de inflação (π)—ou seja, a taxa real de juros (i—π) é constante (Shiller 2001, 260n224). As hipóteses clássica e neoclássica estão em desacordo.

Figura 6.7 - Taxas de Lucro Incremental Corrente Corporativas Corrigidas e Medidas Proxy NIPA (Numericamente, Taxas Correntes = Taxas Reais)

20. A Figura 6.7 faz duas comparações. O primeiro painel compara a taxa de lucro incremental corporativo nominal (iropcorp), calculada usando a razão da variação no GOS nominal corrigido para a soma do investimento bruto nominal em capital fixo e a variação nos estoques nominais, com a medida equivalente da NIPA (iropcorpnipa), calculada como a razão da variação no lucro bruto nominal da NIPA (variação na soma real do lucro líquido e depreciação a custo corrente) para o investimento bruto nominal em capital fixo. Este é um teste dos efeitos das correções no numerador e no denominador, e é de grande interesse descobrir que as duas medidas são praticamente iguais: a taxa de lucro incremental corrigida tem essencialmente a mesma média e um desvio padrão um pouco menor do que a medida mais simples da NIPA. O segundo gráfico compara a taxa de lucro incremental corporativo corrente (real) corrigida (iroprcorp), calculada da mesma forma que a taxa nominal, exceto com variáveis reais, com a taxa da NIPA (iroprcorpnipa), também usando variáveis reais (apêndice 6.8.II.7). Aqui, a medida corrigida tem uma média ligeiramente maior, mas um desvio padrão ligeiramente menor (tabela 6.23). Essas descobertas são bastante importantes porque as medidas da NIPA são facilmente estimadas entre países e ao longo do tempo. Veremos a seguir que as taxas nominais e correntes incrementais das corporações dos EUA da NIPA são muito semelhantes às taxas de retorno correspondentes das ações corporativas dos EUA—uma confirmação direta das expectativas clássicas sobre a equalização das taxas de lucro entre setores e uma validação da importância atribuída aos lucros corporativos pelos analistas de mercado de ações não acadêmicos (capítulo 10).

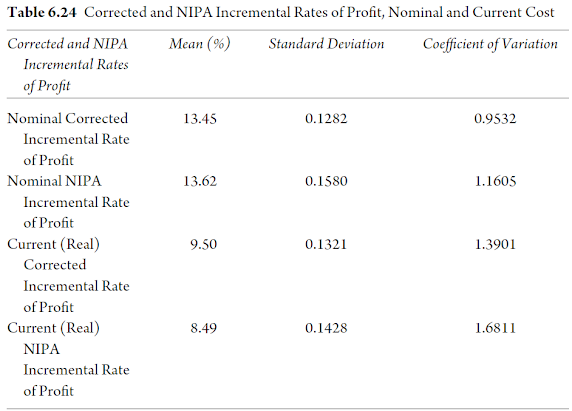
Tabela 6.24 - Taxas de Lucro Incremental Corrigidas e da NIPA, Nominais e a Custo Corrente