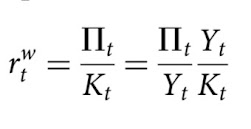O Comportamento da Taxa de Câmbio Real - Martínez-Hernández

MARTÍNEZ-HERNÁNDEZ, Francisco A. The political economy of real exchange rate behavior: Theory and empirical evidence for developed and developing countries, 1960–2010. Review of Political Economy, v. 29, n. 4, p. 566-596, 2017.

Texto completo disponível aqui.

RESUMO

Os resultados empíricos dos testes da hipótese da PPC têm constantemente demonstrado que os preços relativos não convergem para o mesmo nível, tanto no curto prazo quanto no longo prazo. Portanto, a explicação da PPC para a taxa de câmbio real não oferece uma medida razoável de competitividade no nível internacional. Este artigo apresenta uma abordagem diferente com base nos trabalhos de Ricardo, Marx, Harrod e Shaikh. Argumenta-se que o custo real relativo da unidade de trabalho é o principal fator que explica o comportamento de longo prazo da taxa de câmbio real. A segunda seção do artigo explana os fundamentos teóricos de nossa abordagem. A terceira seção analisa o papel do diferencial da taxa de juros real na explicação dos desalinhamentos da taxa de câmbio real. Na quarta seção, apresentamos uma análise gráfica da inter-relação entre a taxa de câmbio efetiva real, a relação de custo real da unidade de trabalho, o diferencial da taxa de juros real de curto prazo e o saldo comercial para 16 países da OCDE, Taiwan e três países em desenvolvimento no período de 1960 a 2010. A quinta seção investiga a relação de longo prazo entre os três últimos índices por meio de modelos de co-integração e correção de erros usando a estrutura ARDL-ECM. A última seção apresenta nossas conclusões.

Introdução

O comércio mundial e as finanças internacionais evoluíram desde os tempos dos economistas políticos clássicos. No entanto, os economistas mainstream ignoraram algumas lições-chave de Karl Marx, Roy Harrod e John Maynard Keynes em relação à compreensão das condições competitivas nacionais e internacionais desiguais sob o capitalismo (por exemplo, o papel das diferenças em tecnologia, diferenciais de salário, rigidez de preços e o papel do dinheiro na produção). No geral, as consequências de um sistema de comércio internacional desigual têm sido o comércio desequilibrado e altos níveis internacionais de endividamento, que impuseram um viés expansionista para países com superávits comerciais e um viés deflacionário para países com déficits comerciais (especialmente para economias pequenas).

Este artigo adota uma teoria de preços fundamentada no pensamento clássico, que leva em consideração o papel da competição intra e interindustrial (competição real), produtividade e salários reais no setor comercializável. As teorias monetárias e comerciais padrão assumem que situações de comércio desequilibrado são temporárias, com base na suposição de que os preços domésticos e externos se moverão de tal maneira a manter uma taxa de câmbio real aproximadamente constante ao longo do tempo. Em vez disso, argumentamos que nossa teoria alternativa de preços pode explicar os termos de troca nacionais e internacionais e nos permite explicar as mudanças na taxa de câmbio real e o grau de competitividade internacional.

Nossa abordagem baseia-se no trabalho de Shaikh (1980, 1991, 1999, 2016). A ideia básica é que, no âmbito da produção manufatureira em nível nacional e internacional, uma vez que o capital e os bens intermediários são negociados nos mercados internacionais, enquanto o trabalho permanece em grande parte imóvel internacionalmente, os custos trabalhistas provavelmente divergirão muito mais entre os países do que outros custos de produção. Portanto, os custos trabalhistas desempenham um papel desproporcionalmente importante na competitividade, na nossa visão. Assim, os custos reais unitários de trabalho na manufatura (custo do trabalho dividido pela produção por trabalhador) capturam um determinante subjacente fundamental da competitividade em bens comercializáveis.

A segunda seção desenvolve nossa abordagem alternativa. Começamos com uma economia fechada e passamos para uma economia aberta. Na terceira seção, baseando-nos principalmente em Marx e Harrod, explicamos por que os desequilíbrios comerciais têm um impacto na liquidez interna das economias e, como consequência, nas taxas de juros domésticas e nas taxas de câmbio reais (em vez dos preços relativos). A quarta seção apresenta uma análise gráfica da inter-relação entre os índices da taxa de câmbio efetiva real, a relação de custo real ajustado da unidade de trabalho, o diferencial da taxa de juros real de curto prazo e o saldo comercial para 16 países da OCDE (Organização para a Cooperação e Desenvolvimento Econômico), Taiwan e três países em desenvolvimento, principalmente para o período de 1960 a 2010. A quinta seção investiga a natureza da relação de longo prazo entre os três índices mencionados anteriormente e o saldo comercial por meio de modelos de co-integração e correção de erros usando a estrutura de mecanismo de correção de erros com defasagem distribuída autorregressiva (ARDL-ECM). A última seção oferece algumas observações finais.

2. Um quadro clássico para análise da taxa de câmbio real

2.1. Teoria da concorrência, taxa de lucro e formação de preços industriais

O ponto de partida para o modelo de taxa de câmbio real de Shaikh é a teoria clássica da concorrência, que pode ser rastreada até os escritos de Smith, Ricardo e Marx. Essa abordagem clássica considera a competição como uma rivalidade entre empresas, onde os produtores tentam obter uma maior parcela do mercado reduzindo custos e cortando preços. Assim, as empresas são vistas como constantemente buscando reduzir custos, principalmente através da supressão do crescimento dos salários reais e da introdução, em intervalos, de melhores técnicas de produção (ou seja, aumento da produtividade devido a mudanças tecnológicas).

A partir desse ponto de vista clássico, a competição real implica que as empresas dentro de uma indústria não necessariamente enfrentam uma estrutura de custos semelhante (ou seja, existem diferenças tecnológicas entre as empresas). Em outras palavras, a 'Lei do Preço Único' (LOP) força as empresas dentro de uma indústria a vender seus produtos no mercado a um preço único, que eventualmente, devido às diferenças nas condições de produção, resultará em diferentes margens de lucro e taxas de lucro para cada empresa em uma dada indústria.

Portanto, a operação da LOP (ignorando custos de transporte, impostos, etc.) criaria uma diferenciação de lucro entre as empresas dentro de uma indústria (concorrência intra-indústria), onde a(s) condição(ões) de produção mais favorável(is) (estrutura de custos mais baixa) obterá uma taxa de lucro maior, porque a posse da melhor técnica produtiva permite ao produtor mais competitivo regular o preço de venda no mercado. Ou seja, o preço que prevalece em um mercado específico não é o preço médio da indústria, mas o preço de menor custo determinado pelo(s) produtor(es) mais eficiente(s) naquela indústria. Esse preço é chamado de preço regulador e o produtor é o capital regulador, em contraste com o preço médio e o capital médio (Ruiz-Nápoles 1996; Shaikh 1999). Por sua vez, os capitais não reguladores serão forçados pela concorrência a vender ao mesmo preço e, como resultado, terão uma variedade de taxas de lucro determinadas por suas próprias diversas condições de produção (Shaikh 1999, p. 2).

Por outro lado, essa "heterogeneidade das taxas de lucro" dentro de uma indústria não passará despercebida por muito tempo. A diferenciação de lucro pode facilmente chamar a atenção de outros capitalistas em outras indústrias, ou seja, outros capitais reguladores, que também estão ansiosos por lucros. Nesse sentido, a tradição clássica pressupõe que a "livre mobilidade de capital" entre diferentes setores industriais (concorrência interindústria) produz a tendência para uma igualação aproximada das taxas de lucro entre os setores de lucro desigual anteriores, particularmente entre os capitais reguladores de diferentes indústrias (Foley 1986; Ge 1993; Guerrero 1995; Antonopoulos 1997; Shaikh 1999; Sarich 2006).

Finalmente, para a perspectiva clássica, o processo dinâmico e turbulento da concorrência intra e interindústria não exige a correspondente igualação das taxas salariais a fim de alcançar uma igualação aproximada das taxas de lucro entre as indústrias (Shaikh 1991, p. 2). Em outras palavras, os fluxos de novos investimentos capitalistas em uma indústria podem ter um impacto significativo na oferta e nos preços sem necessariamente afetar as taxas salariais do setor (não se pressupõe pleno emprego). Onde a mobilidade da mão de obra é restrita por qualquer motivo, os diferenciais salariais podem persistir mesmo que as taxas de lucro estejam igualadas (Shaikh 1991, p. 2; Botwinick 1993, p. 250).

Nesta seção, começamos assumindo que, a nível nacional, a concorrência intra-indústria integra os mercados regionais para qualquer mercadoria dada, de modo que os preços de mercado das mercadorias i ou j serão aproximadamente iguais entre os mercados regionais, assumindo que a LOP se aplica de forma geral. Por outro lado, a concorrência interindústria fará com que os mencionados preços de mercado comuns de Pi e Pj gravitem em torno de seus respectivos preços reguladores de produção, P*i e P*j. Portanto, a longo prazo, temos as Equações 1 e 2:

Ao combinar as Equações 1 e 2, podemos obter a Equação 3. Da Equação 3 segue que, a longo prazo, a relação de qualquer troca entre as mercadorias i e j (ou seja, os termos de troca domésticos na economia) será aproximadamente igual aos preços reguladores relativos desses conjuntos de mercadorias.

A Equação 3 acima também mostra que, dentro de uma nação, devido à concorrência interindústria, os preços relativos de produção dos produtos i e j são determinados pelo produtor de melhores práticas; ou seja, o produtor regulador (Ge 1993, p. 254). A questão importante com relação à Equação 3 é compreender os principais determinantes do nível desses preços e entender suas implicações no que diz respeito à explicação dos termos de troca nacionais de longo prazo. Para resolver essas questões, Shaikh (1984, 2016) reformula a apresentação do sistema de preços de Pasinetti (1977) para mostrar que os preços relativos em questão podem ser relacionados aos custos unitários; especificamente, aos custos totais unitários de trabalho verticalmente integrados, representados pelas quantidades de trabalho diretamente e indiretamente incorporadas em cada unidade física do sistema de mercadorias (ou seja, o que Karl Marx chamou de 'trabalho vivo e morto' ou valores de trabalho).

Por um lado, Pasinetti (1977, p. 73) considerava o sistema de preços como um em que cada mercadoria é produzida por meio do uso de uma certa quantidade física de trabalho e uma quantidade física dada de mercadorias necessárias como meios de produção. De acordo com isso, o valor agregado no sistema econômico é assumido ser dividido em duas categorias: salários e lucros. Assim, a representação de Pasinetti do sistema de preços pode ser ilustrada da seguinte forma:

Onde p denota o vetor (linha) de preços, w (um escalar) a taxa de salário e π (também um escalar) a taxa de lucro. A representa uma matriz de coeficientes interindustriais (ou uma matriz insumo-produto) e um vetor (linha) de coeficientes de trabalho direto.

Com base na Equação 4, após alguma manipulação algébrica, Pasinetti (1977, pp. 76-77) chegou ao seu sistema de preços geral (Equação 5), onde a taxa de lucro se encontra em algum ponto entre seu valor máximo (Π), que corresponde a uma possibilidade teórica, onde a taxa de salário é zero, e uma taxa de lucro não nula (π̄ ) e uma taxa de salário positiva (w). Aqui, I significa uma matriz identidade.

Com a Equação 5, Pasinetti (1977, p. 81) reinterpretou o modelo insumo-produto de Leontief para mostrar que, de acordo com a teoria de valor de Ricardo, quando na equação acima π̄ = 0 (o produto líquido inteiro, ou excedente do sistema econômico, vai para salários). Nesse caso, os preços se tornam proporcionais às quantidades de trabalho direto e indireto (coeficientes de trabalho verticalmente integrados, v na Equação 6 acima). No entanto, assim que π̄ > 0, esse resultado deixa de ser válido. As quantidades de trabalho indireto ((I - A)-¹) passam a adquirir um maior "peso" em relação às quantidades de trabalho direto (an). Portanto, de acordo com Pasinetti, a proporcionalidade entre preços e quantidades de trabalho incorporado (ou seja, a teoria pura do valor-trabalho) se desfaz sob condições de taxas de lucro positivas.

Por outro lado, Shaikh (1984, 2016) reformulou o sistema de preços de Pasinetti usando a decomposição competitiva de longo prazo de preço de Adam Smith para mostrar que os preços relativos podem ser relacionados aos custos relativos totais unitários de trabalho verticalmente integrados. Em termos formais, essa decomposição de preço (em termos monetários) pode ser ilustrada da seguinte forma: suponhamos que p, u, π e m sejam o preço por unidade, os custos trabalhistas, os lucros brutos e os custos materiais, respectivamente, de alguma mercadoria dada. Então, por definição, podemos escrever p = u + π + m. No entanto, os custos materiais são simplesmente o preço de algum conjunto de insumos materiais (incluindo depreciação), que por sua vez pode ser decomposto em custos unitários de trabalho, lucros e seus próprios custos materiais um estágio (conceitual) anterior. Essa decomposição pode ser repetida nos custos materiais do próprio conjunto de materiais e assim por diante, de modo que, sem perda de generalidade, a decomposição competitiva de longo prazo de preço de Adam Smith pode ser representada como (Shaikh 1984, p. 65, 2016, p. 386):

Na Equação 7, o novo custo material (residual) m(¹) é menor do que o custo material original m. Além disso, se repetirmos o processo acima, podemos reduzir m(¹) aos seus custos trabalhistas, lucros e custos materiais, de modo que m(1) = u(²) + π(²) + m(²), e então reduzir esse custo material remanescente aos seus componentes, até que, no limite, não haja custo material residual algum. Dessa forma, independentemente de como o preço seja determinado na realidade, sempre podemos expressá-lo como uma série infinita de salários e lucros em estágios conceitualmente recuantes de produção (Shaikh 1984, p. 66).

Nesse sentido, podemos denotar a soma de todos os custos unitários de trabalho diretos e indiretos (verticalmente integrados) como v = u + u(¹) + u(²) + u(³) +··· e a soma de todos os lucros brutos unitários diretos e indiretos (verticalmente integrados) como πT = π + π(¹) + π(²) + π(³) +···. Em seguida, a Equação 7 pode ser reexpressa como:

Onde ρ = πT/v é a média da relação entre lucro direto e indireto (ou seja, verticalmente integrado) e salário.

Aqui, devemos ter em mente que essa decomposição de preço pode ser aplicada a qualquer preço, uma vez que decorre de uma identidade contábil. Portanto, para qualquer duas indústrias i e j, respectivamente, sempre podemos expressar seus preços relativos na forma expressa pela Equação 9, que Shaikh (1984, 2016) chama de Equação Fundamental de Preços:

onde zij = (1 + ρi) / (1 + ρj) = a razão das taxas de lucro direto e indireto (ou seja, verticalmente integrado) entre os dois setores.

A Equação Fundamental de Preços mostra que o preço relativo de qualquer duas mercadorias depende apenas de dois termos: seus custos relativos unitários de trabalho verticalmente integrados e suas margens de lucro bruto verticalmente integrado relativo. Neste ponto, Shaikh (1984), seguindo Ricardo (2004), entrelaça resultados teóricos e empíricos da análise de estruturas verticalmente integradas para supor que o segundo termo da Equação 9, a razão das taxas de lucro direto e indireto verticalmente integradas (zij), pode ser visto como um termo de perturbação com um valor estável em torno de 1. Shaikh assume que, devido à alta interconexão entre os setores industriais, mesmo grandes variações entre ρi e ρj induziriam apenas pequenas variações nos preços relativos em relação aos custos relativos unitários de trabalho verticalmente integrados, de modo que zij não é estruturalmente relevante na explicação do nível de preços relativos de longo prazo [1].

[1]: Vale ressaltar que a suposição de que zij ≅ 1 não requer que todos os setores tenham a mesma relação capital-trabalho ou que a taxa de lucro seja zero. Para uma explicação formal deste ponto, consulte Shaikh (1984, p. 68).

Portanto, a Equação 10 abaixo pode ser considerada uma excelente aproximação da Equação 9.

Portanto, a Equação 10, que reflete a teoria de valor de Ricardo, onde as quantidades relativas de trabalho direto e indireto utilizadas na produção de duas mercadorias regulam o valor de troca dessas mercadorias ao longo do tempo, pode ser considerada uma excelente aproximação para medir os termos de troca nacionais industriais. Na verdade, pesquisas empíricas em nível nacional e internacional baseadas em dados insumo-produto mostraram que os custos unitários de trabalho verticalmente integrados fornecem uma excelente aproximação (da ordem de 85-90 por cento) dos preços relativos (consulte Shaikh 1984; Bienenfeld 1988; Ochoa 1989; Milberg and Elmslie 1992; Ruiz-Nápoles 1996, 2010; Chilcote 1997).

As principais teorias econômicas geralmente aceitam que a competição dentro de um país seja regulada pelo princípio da vantagem absoluta em custos (Guerrero 1995, p. 20; Féliz and Sorokin 2008, p. 290). No entanto, como observado por Harrod (1957, Capítulo VI) e Shaikh (1980, 1991), quando se trata de comércio internacional, a teoria neoclássica abandona o princípio dos custos absolutos como a principal força motriz da competição internacional e substitui pelo princípio dos custos comparativos. Sob a teoria dos custos comparativos, os países tenderão a se especializar na produção daqueles bens que produzem relativamente mais barato. De acordo com essa lógica, nações menos desenvolvidas tenderão a se especializar na produção de bens onde têm uma relação custo-preço relativamente menor, mesmo que produzam esses bens de forma ineficiente ou de maneira mais cara do que outras nações avançadas (Salgado, Góchez e Bolaños 2010).

Além disso, do ponto de vista da teoria da vantagem comparativa, uma vez que o comércio internacional ocorre, assume-se que qualquer desequilíbrio comercial que possa ocorrer inicialmente deveria eventualmente desaparecer por meio de ajustes nos preços domésticos e externos, independentemente da posição competitiva absoluta de cada país (ou seja, ajuste por meio da taxa de câmbio real). Ou seja, quando os modelos de comércio neoclássicos aceitam o mecanismo de fluxo de preços-espécie de Hume (que se baseia na teoria quantitativa da moeda) e a teoria de 'demanda nacional recíproca' de J. S. Mill, eles assumem que cada país sempre seria forçado a manter uma taxa de câmbio real aproximadamente constante e um equilíbrio comercial equilibrado. Há uma suposição implícita nos modelos de comércio neoclássicos de que os países com influxos de capital líquido (por exemplo, devido ao superávit comercial) terão tendência a ver aumentos nos preços domésticos, enquanto aqueles países com saída líquida de capital (por exemplo, devido ao déficit comercial) terão tendência a experimentar uma redução nos preços domésticos, resultando em um 'mecanismo automático' que tenderia a manter a taxa de câmbio real constante ao longo do tempo (veja Shaikh 1980, p. 216, 2016, p. 502; Sarich 2006, p. 473; Hunt e Lautzenheiser 2011, p. 190; Martínez-Hernández 2015, pp. 10–11).

Para o nosso modelo alternativo de taxa de câmbio real, sob a suposição de livre comércio, a vantagem absoluta seria refletida nos mercados internacionais pela predominância dos preços regulados (pelo produtor regulador) para cada commodity comercializável. Nesse contexto, espera-se que os bens comercializáveis sejam vendidos por aproximadamente o mesmo preço de mercado internacional em todos os países, quando expressos em uma moeda comum, após considerar disparidades que surgem devido a diferenças nos custos de transporte, impostos indiretos e outros fatores relevantes (assumimos que a LOP se aplica) [2]. Assim, os preços de mercado dos capitais reguladores devem se conformar aos custos relativos unitários de trabalho real, verticalmente integrados, das empresas reguladoras (vr).

[2]: Vale ressaltar que, por si só, a LOP não implica uma taxa de câmbio real de equilíbrio de longo prazo (na qual o saldo comercial seria igual a zero), sendo possível que a LOP prevaleça mesmo quando houver superávit ou déficit comercial (veja Antonopoulos 1997, p. 11; Sarich 2006, p. 472).

Nessas circunstâncias, a competitividade internacional, medida por mudanças nos custos unitários de trabalho real verticalmente integrados dos respectivos setores comercializáveis, leva a mudanças nos termos de troca internacionais. Isso sugere que, se os capitais reguladores do país nacional conseguirem reduzir seus custos de produção e, como resultado, seus preços, então, ceteris paribus, é razoável supor que seus termos de troca diminuiriam, depreciando sua taxa de câmbio real e aumentando sua competitividade internacional em relação ao seu concorrente internacional. Alternativamente, na ausência de concorrentes potenciais, reduções nos custos de produção podem ser compensadas por um aumento proporcional nas margens de lucro e, portanto, a taxa de câmbio real permanece inalterada. Em outras palavras, cortes nos custos de produção só levam à depreciação quando há concorrentes potenciais forçando as empresas a não aumentar suas margens.

Competição e Taxas de Câmbio - Anwar Shaikh

Shaikh, A. (1991). Competition and exchange rates: theory and empirical evidence (Working Paper). New York: Deparment of Economics / New School for Social Research.

Texto original em inglês disponível aqui.

RESUMO

Este artigo desenvolve e testa uma teoria de longo prazo da taxa de câmbio baseada em uma abordagem clássica da teoria da concorrência. A teoria subjacente da concorrência permite diferenças de tecnologia entre empresas dentro de uma indústria e fluxos de capital entre indústrias. Primeiramente, é aplicada à competição dentro de uma "nação" (ou seja, uma área integrada de moeda comum) e depois estendida para o caso de múltiplas moedas. O modelo resultante de taxas de câmbio se assemelha à teoria da Paridade do Poder de Compra (PPC) quando as taxas de inflação relativas são altas e/ou quando dois países produzem cestas similares de bens comercializáveis. Entretanto, em outras circunstâncias, diferenciais internacionais de produtividade, salários reais e a relação de preços entre bens comercializáveis e não comercializáveis desempenham um papel importante na determinação do centro de gravidade de longo prazo das taxas de câmbio. A teoria é testada com dados dos Estados Unidos, Japão, Alemanha, Reino Unido e Canadá.

Introdução

Este artigo desenvolve e testa uma teoria de longo prazo da taxa de câmbio com base em uma abordagem clássica da teoria da concorrência. O modelo resultante de taxas de câmbio se assemelha à teoria da Paridade do Poder de Compra (PPC) quando as taxas de inflação relativas são altas e/ou quando dois países produzem cestas similares de bens. No entanto, em outras circunstâncias, a produtividade, a relação de preços entre bens comercializáveis e não comercializáveis e os salários reais desempenham um papel importante na determinação do centro de gravidade de longo prazo das taxas de câmbio.

A seguir, desenvolveremos inicialmente a teoria subjacente da concorrência conforme ela se aplica a uma "área de moeda comum" integrada, e então estenderemos seus argumentos para o caso de múltiplas moedas. Esse último passo resulta em uma teoria específica da taxa de câmbio de longo prazo, cujas implicações são distintas das de outras teorias. Concluiremos testando a teoria com dados dos Estados Unidos, Japão, Alemanha, Reino Unido e Canadá.

I. A teoria da concorrência

A competição industrial consiste em dois processos distintos: a igualação aproximada dos preços de venda dentro de uma indústria para todos os bens geralmente comercializáveis, modificada por custos de transporte, impostos, etc; e a igualação aproximada das taxas de lucro entre indústrias, causada pela resposta do investimento às diferenças interindustriais nas taxas de lucro.

A competição intra-industrial faz com que os preços de venda individuais de um determinado bem geralmente comercializável gravitem em torno de algum preço comum. No entanto, porque a Lei (aproximada) de Um Preço (LOP) resultante é válida para qualquer preço comum dentro de uma indústria, ela não fornece uma teoria para o nível desse preço comum. Um processo adicional é necessário.

A economia clássica fechou a teoria argumentando que a competição interindustrial leva à igualação aproximada das taxas de lucro entre indústrias. Esse segundo processo (e provavelmente mais lento) faz com que o preço comum estabelecido pela LOP também se mova em torno de um preço de longo prazo que os Clássicos chamavam de "preço natural" e que Marx chamava de "preço de produção". Uma vez que desejo usar o termo "gravitar" no sentido orbital em vez de no sentido de convergência eventual, usarei este último termo em vez do termo mais comum "preço de equilíbrio de longo prazo".

É importante reconhecer que os dois processos acima não são imediatamente congruentes. A competição intra-industrial força as empresas dentro de uma indústria a vender a preços aproximadamente comuns (após consideração dos custos de transporte e impostos locais). No entanto, isso significa que as diferenças entre as estruturas de custo dessas empresas se refletirão como diferenças nas margens de lucro intra-industriais e nas taxas de lucro. Assim, a Lei de Um Preço tende a desigualar margens de lucro e taxas de lucro entre as empresas dentro de uma dada indústria [1].

[1] Empresas com custos unitários mais baixos terão margens de lucro mais altas a qualquer preço de venda comum. Na medida em que os custos unitários mais baixos se devem a métodos de produção mais capitalizados, refletidos em maiores índices de capital-produção (em níveis normais de utilização da capacidade), as diferenças nas taxas de lucro dentro de uma indústria serão menores do que as diferenças nas margens de lucro (pois a taxa de lucro em capacidade normal é a margem de lucro nas vendas dividida pelo índice de capital-produção, ambos em níveis normais de utilização da capacidade).

Por outro lado, os fluxos de investimento entre indústrias são motivados pelas taxas de retorno esperadas para novos capitais nessas indústrias. Uma vez que os capitais existentes dentro de uma indústria terão diferentes taxas de lucro a qualquer preço comum, por razões indicadas acima, qual destes servirá como indicador para novo investimento? A resposta, eu argumentaria, é a taxa de lucro (esperada) do melhor (ou seja, de menor custo) método de produção geralmente disponível em qualquer indústria. Esses métodos de produção reguladores são aqueles que os capitais recém-entrantes tenderão a adotar. Chamarei os capitais que incorporam esses métodos de capital os capitais reguladores para cada indústria. Para que as taxas de lucro sejam igualadas entre as indústrias, é necessário apenas que novos investimentos acelerem em relação à demanda nas indústrias com taxas de lucro reguladoras acima da média e desacelerem em relação à demanda naquelas com taxas abaixo da média [2]. Tais taxas diferenciais de investimento reduzirão os preços nas indústrias anteriores em relação às últimas. O resultado final é um processo que faz com que o preço médio de cada indústria gravite em torno de um nível que produz uma taxa de lucro aproximadamente normal para os capitais reguladores dessa indústria.

Três pontos adicionais são importantes. Primeiro, a formação de um preço comum entre empresas dentro de uma indústria não requer incursões reais (ou seja, "exportações" e "importações") nos territórios uns dos outros. Para bens geralmente comercializáveis, a ameaça de tais incursões e/ou a existência de fornecedores e compradores comuns são suficientes (McCloskey e Zecher 1985:66). Da mesma forma, a formação de taxas de lucro aproximadamente iguais entre capitais reguladores em diferentes indústrias não requer fluxos de capital reais de uma indústria (ou região) para outra. É suficiente que haja taxas diferenciais de investimento (de fontes internas ou externas) ligadas a diferenças nas taxas de lucro (esperadas).

[2] Uma vez que a demanda geralmente estará em crescimento, os movimentos envolvidos são relativos à tendência, ou seja, acelerações ou desacelerações.

Segundo, a equalização das taxas de lucro entre as indústrias não exige a equalização correspondente das taxas salariais. Fluxos de novo capital para uma indústria podem ter um impacto significativo na oferta e no preço sem necessariamente afetar as taxas salariais locais. Onde a mobilidade da mão-de-obra é restrita por qualquer motivo, diferenciais salariais podem persistir mesmo que as taxas de lucro estejam igualadas (Botwinick 1988).

Terceiro, novos fluxos de investimento em uma indústria trazem constantemente novos métodos e substituem os antigos. Em um contexto dinâmico, isso inevitavelmente leva a uma variedade de gerações dentro de cada indústria, cuja distribuição se estreitará ou se alargará com as mudanças nas taxas de investimento e no progresso técnico. Isso explica a suposição anterior de que mesmo a competição será caracterizada por diferenças persistentes nos métodos de produção dentro de qualquer indústria específica.

Salários, Desemprego e Estrutura Social: uma nova curva de Phillips - Anwar Shaikh

Shaikh, Anwar. 2013. Wages, unemployment and social structure: A new Phillips curve. Global & Local Economic Review 17 (2): 5–19.

Texto original em inglês disponível aqui.

Resumo

Existem várias teorias econômicas sobre a relação inerente entre emprego e inflação, assim como as conexões com outras variáveis econômicas.

A hipótese clássica propõe uma relação entre a taxa de variação da parcela salarial e o desemprego. A curva de Phillips original demonstra que os salários monetários aumentam de maneira não linear quando o desemprego está abaixo de certos níveis críticos e caem de maneira semelhante quando o desemprego está acima desse nível. Além disso, vários estudiosos demonstram através de análises empíricas tal relação para diferentes séries temporais. Este artigo apresenta um estudo sobre dados dos EUA considerando dados de emprego e variação salarial de maneira diferente e mais eficiente. Mudanças significativas são destacadas nos períodos históricos considerados.

1. Introdução

A economia Pré-Keynesiana era caracterizada pela noção familiar de equilíbrio simultâneo em todos os mercados, incluindo o pleno emprego dos trabalhadores no mercado de trabalho. Supunha-se que todos os preços funcionassem apenas como variáveis que ajustam o mercado. Essa atribuição também se estendia ao mercado de trabalho, no qual salários reais competitivos eram considerados apenas como variáveis de ajuste do mercado de trabalho, tendo como única função manter o pleno emprego. Os trabalhadores, sem dúvida, negociavam por salários reais para alcançar um padrão de vida, mas no final o padrão de vida que obtinham era aquele que garantia seu próprio pleno emprego. Em uma economia perfeitamente competitiva, a luta entre trabalho e capital não desempenhava papel na determinação do salário real de equilíbrio (Shaikh, 2003, p. 129-132; Snowdon e Vane, 2005, pp. 37-54).

Keynes também se baseou em mercados competitivos, já que acreditava que mesmo a "concorrência atomística" poderia resultar em desemprego persistente (Leijonhufvud, 1967, p. 403) [1]. No entanto, em seu caso, as negociações salariais e as lutas trabalhistas desempenhavam um grande papel. Ele estava bem ciente da alegação neoclássica de que o desemprego reduziria o salário real, aumentaria a lucratividade e, assim, levaria o sistema de volta ao pleno emprego. De fato, após a publicação da Teoria Geral, ele admitiu que o desemprego persistente corroeria não apenas os salários monetários, mas também os salários reais (Bhattacharjea, 1987, pp. 276-279), de modo que, eventualmente, a lucratividade, o investimento, a produção e, portanto, o emprego aumentariam. No entanto, no ínterim, em uma sociedade caracterizada por negociações salariais descentralizadas, cada redução salarial teria que ser disputada localmente, o que resultaria em "lutas inúteis e desastrosas" que não poderiam ser justificadas sob argumentos sociais (Snowdon e Vane, 2005, p. 66, citando Keynes). Portanto, ele argumentou que em uma crise seria muito melhor que o Estado se engajasse em políticas fiscais para aumentar diretamente a demanda agregada e o emprego.

Taxas de Lucro Mundiais (1960 - 2019) - Deepankar Basu et al.

Deepankar Basu, Julio Huato, Jesus Lara Jauregui & Evan Wasner (2022): World Profit Rates, 1960–2019, Review of Political Economy, DOI: 10.1080/09538259.2022.2140007

Texto original em inglês aqui.

Sumário:

1. Introdução

2. Dados

    2.1. A EPWT7

    2.2. A SEA-WIOD

3. Construção da Taxa de Lucro Mundial

    3.1. Agregando Dados de Países da EPWT7

        3.1.1. Taxa de Lucro Mundial como Média Ponderada de Taxas de Lucro por País

    3.1.2. Decomposição da Taxa de Lucro Mundial

4. Taxas de Lucro em Nível de País: Tendências na Rentabilidade Mundial

    4.1. Rentabilidade Mundial Usando Todas as Observações

    4.2. Rentabilidade Mundial Usando um Conjunto de Dados de Painel Balanceado

5. Taxas de Lucro por Indústria: Tendências na Rentabilidade Mundial

6. Painel de Rentabilidade Mundial

7. Conclusão

Resumo

Neste artigo, apresentamos estimativas da taxa mundial de lucro (líquida) usando dados ao nível dos países da Extended Penn World Table  7.0 e estimativas da taxa mundial de lucro (bruta) usando dados ao nível da indústria da World Input Output Database. A série da taxa de lucro mundial agregada por país abrange o período de 1960 a 2019, e a série da taxa de lucro mundial agregada por indústria abrange o período de 2000 a 2014. A série da taxa de lucro mundial agregada por país exibe uma forte tendência linear negativa no período de 1960 a 1980 e uma tendência linear negativa mais fraca de 1980 a 2019. Uma análise de decomposição de médio prazo revela que a queda na taxa de lucro mundial é impulsionada por uma queda na relação produção-capital. A série da taxa de lucro mundial agregada por indústria mostra uma tendência linear negativa no período de 2000 a 2014, que, mais uma vez, é impulsionada por uma queda na relação produção-capital. Criamos um Painel de Rentabilidade Mundial para permitir que os pesquisadores acessem livremente a série de taxa de lucro mundial e os dados subjacentes nos níveis de agregação por país, indústria, grupo de países e mundial.

Introdução

Este artigo apresenta estimativas das taxas de lucro mundial desde 1960. Dois fatos importantes motivam a pesquisa relatada neste artigo. Primeiro, o capitalismo é um sistema inerentemente global e precisa ser estudado em nível global, em vez de nível nacional, sempre que possível. Segundo, o capitalismo é um sistema de produção social que é regido pela geração e realização de lucro. Portanto, a taxa de lucro é um dos parâmetros-chave que capturam a dinâmica do capitalismo. Unindo essas duas percepções, sugere-se que é importante estimar e estudar as taxas de lucro globais ou mundiais. Isso é precisamente o propósito deste artigo.

Embora os estudiosos reconheçam a importância das taxas de lucro globais, dificuldades de dados e questões metodológicas impediram estudos anteriores de estimar as taxas de lucro mundiais para um grande grupo de países. Um dos primeiros estudos a relatar uma taxa de lucro mundial foi o de Li, Xiao e Zhu (2007). Neste estudo, os autores tentaram estimar uma taxa de lucro mundial remontando ao século XIX usando dados de várias fontes nacionais. Embora o período de tempo de seu estudo seja longo, o número de países incluídos em sua amostra é pequeno, variando entre 3 (para o século XIX) e 6 (após 1963). Roberts (2012) apresenta estimativas de uma taxa de lucro mundial usando 11 países principais, os países do G7 e os 4 países do BRIC. Roberts (2012) usou dados das Tabelas Mundiais Penn Estendidas e apresenta médias ponderadas e não ponderadas das taxas de lucro em nível de país como estimativa da taxa de lucro mundial, um método comum na literatura. Maito (2014) apresenta estimativas de uma taxa de lucro mundial ao agregar dados de fontes nacionais para 14 grandes países capitalistas. Roberts (2015) revisita seus cálculos anteriores, amplia sua amostra de países e período de tempo e reestima uma taxa de lucro mundial para o grupo de países do G20 usando dados das Tabelas Mundiais Penn. Construindo sobre esse trabalho anterior, Maito (2018) apresenta estimativas de uma taxa de lucro mundial ao agregar 14 países, tanto do núcleo quanto da periferia. Ele apresenta médias ponderadas e não ponderadas das taxas de lucro em nível de país como sua estimativa da taxa de lucro mundial.

Estendemos a literatura existente sobre as taxas de lucro mundiais de várias maneiras. Primeiro, derivamos uma fórmula simples para agregar as taxas de lucro em nível de país em uma taxa de lucro mundial. Usando essa fórmula, vemos que a taxa de lucro mundial é uma média ponderada das taxas de lucro em nível de país, com a participação de um país no estoque mundial de capital sendo o peso. Isso implica que estudos anteriores como os de Roberts (2012) e Maito (2018) que usaram o PIB para ponderar as taxas de lucro em nível de país usaram uma metodologia de agregação incorreta. Segundo, usamos duas fontes de dados diferentes: a versão mais recente das Tabelas Mundiais Penn Estendidas (EPWT 7.0) e as Contas Socioeconômicas do Banco de Dados Mundial de Insumo-Produto. Portanto, nossa amostra básica de países é muito maior do que todos os estudos existentes, e nosso conjunto de dados abrange o período de 1960 a 2019.

Terceiro, usamos duas taxas de câmbio diferentes para converter variáveis em nível nacional expressas em unidades de moeda local em uma unidade comum: taxas de câmbio de paridade do poder de compra (PPP) atuais e taxas de câmbio nominais. O uso de taxas de câmbio nos permite calcular adequadamente as taxas de lucro mundiais, garantindo que adicionemos quantidades comparáveis.

Quarto, criamos um Painel de Rentabilidade Mundial para acompanhar este artigo [1]. Os pesquisadores podem usar o painel para visualizar gráficos de séries temporais e decomposições de médio prazo das taxas de lucro em diferentes níveis de agregação, começando do nível de país ou setor até os níveis de grupos de países e finalmente ao nível mundial. O conjunto de dados completo usado para construir esses gráficos e tabelas está disponível para download em diversos formatos.

[Nota 1]: O painel de rentabilidade mundial está disponível aqui: https://dbasu.shinyapps.io/World-Profitability/

Considerando as limitações decorrentes da disponibilidade de dados sobre variáveis de lucratividade e taxas de câmbio, construímos duas séries diferentes de lucratividade mundial. Nossa primeira medida agrega as taxas de lucro em nível de país usando taxas de câmbio PPP; nossa segunda medida usa taxas de câmbio nominais para agregação. Calculamos cada uma dessas duas medidas em dados de nível de país e setor usando todas as observações e um painel balanceado.

Todas as nossas medidas da taxa de lucro mundial exibem tendências semelhantes. Durante todo o período da amostra, 1960–2019, há uma tendência linear negativa nas séries de taxa de lucro mundial. Portanto, há uma queda incondicional na taxa de lucro mundial nos últimos 60 anos. Uma decomposição de médio prazo da mudança na taxa de lucro mostra que a queda na taxa de lucro foi impulsionada pela queda na relação produção-capital, enquanto a parcela de lucro aumentou.

Quando dividimos o período da amostra em dois subperíodos, 1960–1980 (capitalismo regulado) e 1981–2019 (capitalismo neoliberal), vemos a mesma tendência básica, embora com diferentes graus de declínio. No período regulado, a taxa de lucro caiu acentuadamente, impulsionada pela queda na relação produção-capital. No período neoliberal, a taxa de lucro mundial se recuperou por algumas décadas antes de declinar novamente. Durante todo o período neoliberal, a taxa de lucro mundial exibe uma tendência linear fraca e negativa, ou seja, a taxa de lucro mundial diminuiu. A queda é, mais uma vez, impulsionada pela queda na relação produção-capital.

O restante do artigo está organizado da seguinte forma. Na próxima seção, discutimos nossas fontes de dados; na seção seguinte, discutimos nossa metodologia para construir taxas de lucro mundiais; na próxima seção, apresentamos estimativas de taxas de lucro mundiais, discutimos sua evolução temporal e relatamos os resultados de uma decomposição de médio prazo da taxa de lucro na parcela de lucro e na relação produção-capital; na penúltima seção, apresentamos o Painel de Rentabilidade Mundial e fornecemos links para acessá-lo; na seção final, concluímos o artigo com algumas reflexões sobre pesquisas futuras. Em um Apêndice Online, fornecemos a lista de países e setores abrangidos pelos conjuntos de dados que usamos para nossas análises; também fornecemos gráficos mostrando a distribuição temporal das taxas de lucro em nível de país e setor.

2. Dados

As medidas de taxas de lucro mundial apresentadas neste artigo são construídas usando dados de dois conjuntos de dados principais:

. a Tabela Mundial Penn Estendida 7.0 (EPWT7) [2] e

. as Contas Socioeconômicas do Banco de Dados Mundial de Insumo-Produto (SEA-WIOD) [3].

Para agregação global e por grupo, a classificação de países de julho de 2015 do Banco Mundial fornecida pelo Banco Mundial [4] e as estimativas de taxas de câmbio e PPP da OCDE [5] foram utilizadas.

2.1. A EPWT7

A EPWT é um conjunto de dados sobre crescimento econômico montado e mantido por Adalmir Marquetti. As séries de dados na EPWT vêm das Tabelas Mundiais Penn e de algumas outras fontes. Os dados na EPWT são registrados em frequência anual. Várias versões da EPWT estão disponíveis e utilizamos a versão mais recente, ou seja, a versão 7.0. O subconjunto da EPWT7 usado aqui contém dados anuais completos (8116 observações) sobre

. produto interno bruto (preços nacionais atuais),

. estoque de capital (preços nacionais atuais) e

. parcela do trabalho,

para 170 países ao longo de (no máximo) 70 anos (1950-2019) [6].

[Nota 02]: Para detalhes, consulte Marquetti, Morrone e Miebach (2021).

[Nota 03]: Uma descrição detalhada das fontes de dados e dos métodos de estimativa é fornecida em Timmer et al. (2015).

[Nota 04]: Para detalhes, consulte WB (2021).

[Nota 05]: Para detalhes, consulte OECD (2021).

[Nota 06]: Para uma lista de países, consulte o Apêndice Online.

As estatísticas do produto interno bruto são retiradas da Tabela Mundial Penn 10 original, enquanto os estoques de capital são estimados novamente usando a metodologia do Inventário Perpétuo. Agregamos as taxas de lucro em nível de país para calcular a série de taxas de lucro mundial. Discutimos os detalhes de nossa metodologia de agregação na próxima seção.

2.2. A SEA-WIOD

O WIOD abrange 43 países e 56 setores classificados de acordo com a Classificação Internacional Padrão de Atividades Econômicas revisão 4 [7]. A SEA é uma parte do WIOD e contém dados em nível de indústria sobre emprego, estoques de capital, produção bruta e valor adicionado a preços correntes e constantes. O subconjunto do conjunto de dados SEA-WIOD usado neste trabalho contém dados anuais completos (564.240 observações) sobre

. valor adicionado bruto (preços básicos nacionais atuais),

. estoque de capital (preços básicos nacionais atuais) e

. parcela do trabalho no valor adicionado bruto,

para 56 setores/indústrias em 42 países ao longo de (no máximo) 15 anos (2000-2014) [8]. Agregamos os dados da SEA-WIOD em duas etapas, primeiro entre países e depois entre indústrias. Discutimos os detalhes de nossa metodologia de agregação na próxima seção.

[Nota 7]: Para detalhes, consulte https://www.rug.nl/ggdc/valuechain/wiod/

[Nota 8]: Para uma lista de indústrias e países, consulte o Apêndice Online.

3. Construção da Taxa de Lucro Mundial

Construímos séries de taxas de lucro mundiais de duas maneiras. Primeiro, usamos dados em nível de país da EPWT7 e agregamos por países, usando taxas de câmbio PPP ou nominais, para construir uma série de taxas de lucro mundiais. Segundo, usamos dados em nível de país e indústria da SEA-WIOD e construímos séries de taxas de lucro mundiais em duas etapas. Na primeira etapa, agregamos entre países para cada indústria para calcular as taxas de lucro mundiais para cada indústria. Na segunda etapa, agregamos todas as indústrias para calcular uma série de taxas de lucro mundiais.

3.1. Agregando Dados de Países da EPWT7

Seja j = 1, 2, ... , N o índice dos países em nossa amostra. Usando dados em nível de país sobre lucro líquido e estoque de capital, queremos calcular uma taxa de lucro mundial. No ano t, a taxa de lucro mundial é definida como

onde Πt e Kt são o lucro líquido mundial e o estoque de capital mundial, respectivamente, no ano t. [9] O lucro líquido mundial e o estoque de capital, Πt e Kt, são, por sua vez, a soma das variáveis correspondentes em nível de país,

[Nota 9]: O lucro líquido é igual ao lucro bruto menos a depreciação do estoque de capital.

e

onde j = 1, 2, ... , N indexa os países na amostra.

Usamos duas maneiras diferentes de agregar variáveis em nível de país para uma medida da variável em nível mundial. Primeiro, usamos taxas de câmbio PPP para converter todas as variáveis em nível de país medidas em unidades de moeda local em dólares PPP atuais. Segundo, usamos taxas de câmbio nominais para converter todas as variáveis em moeda local em dólares americanos. Em ambos os casos, somos capazes de adicionar de forma significativa o lucro líquido e o estoque de capital entre os países e chegar ao lucro líquido mundial Πt e ao estoque de capital mundial Kt.

3.1.1. Taxa de Lucro Mundial como Média Ponderada de Taxas de Lucro por País

Podemos relacionar a taxa de lucro mundial com as taxas de lucro em nível de país da seguinte maneira:

onde αjt = (Kjt/Kt) é a participação do país j no estoque de capital mundial, e Πjt = (Pjt/Kjt) é a taxa de lucro no país j no ano t. Portanto, a taxa de lucro mundial é uma média ponderada das taxas de lucro em nível de país, onde a participação de um país no estoque de capital mundial é usada como peso. Isso mostra que é incorreto agregar as taxas de lucro em nível de país usando o produto interno bruto (PIB) como pesos. Portanto, estudos anteriores como os de Roberts (2012) e Maito (2018), que utilizaram o PIB para calcular médias ponderadas de taxas de lucro em nível de país, utilizaram um esquema de ponderação incorreto.

3.1.2. Decomposição da Taxa de Lucro Mundial

A taxa de lucro mundial pode ser decomposta em dois componentes,

onde Yt é a produção líquida, o primeiro componente do lado direito, ∏t/Yt, é a parcela de lucro mundial, e o segundo componente do lado direito, Yt/Kt, é a relação produção-capital mundial[10]. Ao longo de qualquer período de tempo, a taxa de crescimento da taxa de lucro, gr, é, portanto, a soma da taxa de crescimento da parcela de lucro, gP/Y, e da taxa de crescimento da relação produção-capital, gY/K, ou seja,

[Nota 10]: A produção líquida é igual à produção bruta menos a depreciação do estoque de capital.

Esta é uma decomposição útil da mudança na taxa de lucro ao longo de qualquer período de tempo e tem sido amplamente utilizada na literatura marxista (Basu e Vasudevan 2013; Basu e Das 2018). Ela decompõe convenientemente a taxa de crescimento da taxa de lucro em um componente que captura a distribuição de renda entre trabalho e capital, a parcela de lucro, e outro que captura fatores tecnológicos, a relação produção-capital. Usaremos essa decomposição abaixo quando apresentarmos nossos resultados sobre as mudanças na taxa de lucro.

Cada um dos dois componentes da taxa de lucro pode ser visto, por sua vez, como médias ponderadas das correspondentes variáveis em nível de país. A parcela de lucro mundial pode ser expressa como

onde βjt = (Yjt/Yt) é a participação do país j na produção mundial, e ∏jt = (Pjt/Yjt) é a parcela de lucro no país j no ano t. Portanto, a parcela de lucro mundial é uma média ponderada das parcelas de lucro em nível de país, onde a participação de um país na produção mundial é usada como peso. A relação produção-capital mundial pode ser expressa como

onde αjt = (Kjt/Kt) é a participação do país j no estoque de capital mundial, e ∏jt = (Yjt/Kjt) é a relação produção-capital no país j no ano t. Portanto, a relação produção-capital mundial é uma média ponderada das relações produção-capital em nível de país, onde a participação de um país no estoque de capital mundial é usada como peso.

A agregação dos dados de país e indústria ocorre em duas etapas. Na primeira etapa, agregamos entre países para gerar as taxas de lucro em nível de indústria mundial; na segunda etapa, agregamos as taxas de lucro em nível de indústria mundial entre todas as indústrias para calcular a taxa de lucro mundial.

Seja i = 1, 2, ... , H o índice das indústrias e j = 1, 2, ... , N o índice dos países na amostra. Usando dados sobre lucro líquido e estoque de capital em nível de indústria em cada país, queremos, na primeira etapa, calcular uma taxa de lucro global ou mundial para cada indústria. No ano t, a taxa de lucro mundial para a indústria i é calculada como

onde ∏it e Kit são o lucro bruto mundial e o estoque de capital mundial, respectivamente, no ano t para a indústria i. [11] O lucro líquido mundial e o estoque de capital em nível de indústria i, ∏it e Kit, são definidos como a soma em todos os países do lucro líquido nessa indústria.

[Nota 11]: A SEA-WIOD não fornece informações sobre a depreciação do estoque de capital. Portanto, trabalhamos com o lucro bruto quando usamos os dados de país e indústria da SEA-WIOD.

e a soma em todos os países do estoque de capital nessa indústria.

onde j = 1, 2, ... , N indexa os países na amostra. Como antes, para cada país, o lucro líquido e o estoque de capital na indústria i, ∏ijt e Kijt, são medidos em dólares PPP atuais (quando as taxas de câmbio PPP são usadas para conversão) ou em dólares americanos atuais (quando as taxas de câmbio nominais são usadas para conversão). Isso nos permite somar de forma significativa o lucro líquido e o estoque de capital entre os países para a indústria i e chegar ao lucro líquido global ∏it e ao estoque de capital global Kit para a indústria i.

Na segunda etapa, agregamos entre indústrias para calcular a taxa de lucro mundial como

Usando um argumento similar ao usado na subseção anterior, podemos ver que a taxa de lucro mundial é uma média ponderada das taxas de lucro em nível de indústria, onde o peso de uma indústria é sua participação no estoque de capital mundial. A análise de decomposição em médio prazo dessa taxa de lucro mundial funciona exatamente como antes, com a taxa de crescimento da taxa de lucro sendo igual à soma das taxas de crescimento da parcela de lucro e da relação produção-capital.

4. Taxas de Lucro em Nível de País: Tendências na Rentabilidade Mundial

Enfrentamos dois problemas relacionados aos dados ao agregar as taxas de lucro em nível de país para uma taxa de lucro mundial. O primeiro problema surgiu devido à variabilidade da disponibilidade de dados país-ano no EPWT 7.0, e o segundo problema veio da disponibilidade de dados de taxas de câmbio - tanto taxas de câmbio nominais quanto taxas de câmbio PPP.

O número variável de países com dados para calcular as taxas de lucro em nível de país nos forçou a pensar em pelo menos duas estratégias diferentes de agregação para calcular a taxa de lucro mundial. Na primeira estratégia, usamos todos os países para os quais os dados estão disponíveis em qualquer ponto no tempo para calcular a taxa de lucro mundial. Essa estratégia tem a vantagem de utilizar todos os dados disponíveis em cada ponto no tempo. Ela também tem a desvantagem de que os países usados para calcular a taxa de lucro mundial variam ao longo do tempo, levantando questões de comparabilidade entre os anos. Para abordar essa questão de comparabilidade, adotamos uma segunda estratégia de agregação.

Na segunda estratégia, usamos um painel equilibrado de países para agregar as taxas de lucro em nível de país para a taxa de lucro mundial. O painel equilibrado consiste em todos os países para os quais os dados estão disponíveis para todos os anos de 1950 a 2019. Essa estratégia tem a vantagem de que o mesmo grupo de países é usado em cada ponto para calcular a taxa de lucro mundial.

Portanto, a taxa de lucro mundial pode ser facilmente comparada ao longo dos anos. No entanto, tem a desvantagem de não utilizar todos os dados disponíveis em qualquer ponto no tempo.

Para agregar os lucros líquidos, os valores adicionados e os estoques de capital em nível de país para as respectivas variáveis mundiais, precisamos expressar todas as variáveis em nível de país (denominadas em unidades de moeda local) em termos de uma unidade comum. Fazemos isso de duas maneiras. Primeiro, usamos a taxa de câmbio PPP para converter as unidades de moeda nacional em dólares americanos equivalentes atuais; segundo, usamos a taxa de câmbio nominal para converter as unidades de moeda local em dólares americanos. Dados sobre ambas as taxas de câmbio PPP e nominais estão disponíveis a partir de 1960. Isso limita nossas séries de taxa de lucro mundial ao período de 1960 a 2019. Só podemos começar em 1960 porque os dados das taxas de câmbio não estão disponíveis antes desse ano; temos que parar em 2019 porque o EPWT 7.0 para nesse ano.

4.1. Rentabilidade Mundial Usando Todas as Observações

Apresentamos gráficos de séries temporais da taxa de lucro líquida mundial calculada com todas as observações disponíveis em qualquer ano nas Figuras 1 e 2. Na Figura 1, a agregação utilizou taxas de câmbio PPP; na Figura 2, usamos taxas de câmbio nominais para a agregação [12].

[Anota 12]: Para ver a evolução temporal da distribuição (média, mediana, desvio padrão e intervalo interquartil) das taxas de lucro líquido em nível de país, consulte o Apêndice Online.

Ambas as séries de taxa de lucro mundial, ou seja, aquela calculada com taxas de câmbio PPP e aquela calculada com taxas de câmbio nominais, exibem tendências semelhantes ao longo do tempo. A taxa de lucro mundial ficou em torno de 10% no início da década de 1960. Pelas duas décadas seguintes, a taxa de lucro mundial diminuiu continuamente e atingiu seu valor mais baixo, em torno de 8%, no início da década de 1980. A partir de seus níveis mais baixos no início da década de 1980, a taxa de lucro mundial recuperou algum terreno nos anos seguintes. No entanto, essa recuperação foi rapidamente revertida e, no geral, a taxa de lucro mundial exibiu uma tendência fraca e negativa no período desde o início da década de 1990.

Podemos analisar a Tabela 1 (agregando com taxas de câmbio PPP) e a Tabela 2 (agregando com taxas de câmbio nominais) para entender qual dos dois fatores, distribuição de renda (capturada pela parcela de lucro) ou tecnologia (capturada pela relação produção-capital), foi o principal impulsionador por trás do movimento da taxa de lucro mundial. A partir das três primeiras linhas da Tabela 1, vemos que a taxa de lucro diminuiu a uma taxa média anual de -0,34% durante todo o período da amostra, 1960-2019, a uma taxa de -0,99% durante o subperíodo de 1960-1980 e a uma taxa anual de -0,09% durante o subperíodo de 1981-2019. Durante todo o período e durante ambos os subperíodos, a parcela de lucro aumentou, a 0,37%, a 0,03% e a 0,37% ao ano, respectivamente. Portanto, durante ambos os subperíodos, a queda na taxa de lucro mundial foi totalmente impulsionada pelo movimento adverso na tecnologia, capturado pelo crescimento negativo na relação produção-capital, enquanto a distribuição regressiva de renda (aumento na parcela de lucro) impediu uma queda ainda maior na taxa de lucro.

Durante todo o período da amostra, a relação produção-capital mundial diminuiu a uma taxa de -0,72% ao ano; no primeiro subperíodo, de 1960 a 1980, a relação produção-capital mundial diminuiu a uma taxa média anual de -1,02%; durante o segundo subperíodo, de 1981 a 2019, a queda correspondente foi a uma taxa média anual de -0,46%. Obtemos uma imagem muito semelhante se usarmos as três primeiras linhas da Tabela 2 para a análise de decomposição, embora os números reais sejam um pouco diferentes. Portanto, nos abstemos de comentar detalhadamente sobre os resultados na Tabela 2.

4.2. Rentabilidade Mundial Usando um Conjunto de Dados de Painel Balanceado

Apresentamos gráficos de séries temporais da taxa de lucro mundial calculada com um conjunto de dados de painel balanceado de países para os quais há dados disponíveis a cada ano, de 1960 a 2019, nas Figuras 3 e 4 [13]. A imagem da evolução e dos impulsionadores da taxa de lucro mundial que surge do uso de um conjunto de dados de painel balanceado não é muito diferente daquela que obtemos ao usar todas as observações disponíveis em cada ponto no tempo (relatada na subseção anterior).

[Anotação 13]: 3O painel balanceado consiste nos seguintes 25 países: Austrália, Áustria, Bélgica, Canadá, Dinamarca, Finlândia, França, Alemanha, Grécia, Islândia, Irlanda, Itália, Japão, Luxemburgo, México, Países Baixos, Nova Zelândia, Noruega, Portugal, Espanha, Suécia, Suíça, Turquia, Reino Unido, Estados Unidos.

A taxa de lucro mundial diminuiu acentuadamente durante os anos 1960 e 1970, se recuperou levemente nas décadas de 1980 e 1990 e depois voltou a declinar no período atual. Se usarmos taxas de câmbio PPP para a agregação, a recuperação das taxas de lucro nos anos 1980 se mantém por alguns anos na década de 1990, antes de declinar para a década de 2010. Por outro lado, se usarmos taxas de câmbio nominais para a agregação, a recuperação da taxa de lucro nos anos 1980 é rápida mas breve, seguida por um longo período de declínio na taxa de lucro mundial.

A análise de decomposição, apresentada nas 4ª, 5ª e 6ª linhas das Tabelas 1 e 2, não é muito diferente. Seja usando taxas de câmbio PPP para a agregação (Tabela 1) ou taxas de câmbio nominais para a agregação (Tabela 2), vemos um declínio pronunciado na taxa de lucro durante o primeiro período, de 1960 a 1980, e um declínio mais suave ao longo do segundo período, de 1981 a 2019. Ambos os declínios, além disso, são impulsionados principalmente pela diminuição na relação produção-capital [14].

[Nota 14]: Curiosamente, para o painel balanceado, a parcela de lucro diminui, em vez de aumentar, no segundo subperíodo. No entanto, a queda da relação produção-capital supera em muito a queda na parcela de lucro. Portanto, ainda é verdade que o declínio na taxa de lucro é impulsionado principalmente pela queda na relação produção-capital.

5. Taxas de Lucro por Indústria: Tendências na Rentabilidade Mundial

Na Figura 5 (agregação de taxas de câmbio PPP) e na Figura 6 (agregação de taxas de câmbio nominais), apresentamos gráficos de séries temporais da taxa de lucro bruta mundial calculada pela agregação de taxas de lucro por indústria em nível global. A taxa de lucro mundial aumentou de 2000 a 2007 e depois caiu com o início da Grande Recessão. A taxa de lucro mundial se recuperou um pouco quando a Grande Recessão terminou, mas depois declinou posteriormente. Vemos o mesmo padrão, independentemente de usarmos taxas de câmbio PPP ou nominais para a agregação [15].

As últimas linhas nas Tabelas 1 e 2 apresentam os resultados da análise de decomposição de médio prazo. Ao longo de todo o período de 2000 a 2014, a taxa de lucro mundial diminuiu a uma taxa de -0,45% ao ano se a agregação PPP for usada e diminuiu a uma taxa de -0,44% ao ano se a agregação de taxas de câmbio nominais for usada. Em ambos os casos, a queda na taxa de lucro é impulsionada pela queda na relação produção-capital; a parcela de lucro, na verdade, aumentou ao longo do período da amostra. Assim, obtemos uma imagem muito semelhante sobre a variação na taxa de lucro mundial, quer usemos dados de nível de país do EPWT7 ou dados de nível de país-indústria do SEA-WIOD.

[Nota 15]: Para ver a média e a mediana da distribuição de taxas de lucro brutas por indústria em nível global entre 2000 e 2014, consulte o Apêndice Online.

6. Painel de Rentabilidade Mundial

Para disseminar nossas descobertas sobre a rentabilidade mundial e fornecer acesso ao conjunto de dados subjacente a todos os pesquisadores, criamos um Painel de Rentabilidade Mundial [16]. O painel é uma ferramenta conveniente e publicamente disponível para exibir e compartilhar dados com outros pesquisadores, formuladores de políticas e ativistas sobre a rentabilidade global em vários níveis de agregação. Programado com o pacote 'Shiny' do R, o painel oferece aos usuários várias opções para filtrar e exibir os dados. O painel contém duas opções principais para apresentar dados de rentabilidade: nível de indústria e nível de país. O primeiro agrega dados globais para uma indústria específica, enquanto o último agrega dados globais para economias nacionais inteiras. Como o EPWT não desagrega suas variáveis por indústria, apenas o WIOD é usado para cálculos em nível de indústria. Para dados em nível de país, o usuário pode selecionar entre o EPWT e o WIOD. Quando o usuário seleciona o EPWT, a taxa de lucro líquida é calculada; quando o usuário seleciona o WIOD, a taxa de lucro bruta é calculada.

[Nota 16]: O painel de rentabilidade mundial está disponível aqui: https://dbasu.shinyapps.io/World-Profitability/

Uma vez que um usuário tenha selecionado entre dados de nível de indústria e dados de nível de país, o usuário deve escolher ainda entre os seguintes três níveis de agregação, apresentados como abas no painel: 'global', 'por grupo de renda' e 'por país'. A aba 'global' calcula as parcelas de lucro, as razões entre produção e capital e as taxas de lucro para toda a economia global usando todos os países disponíveis no conjunto de dados fornecido. A aba 'por grupo de renda' calcula as mesmas variáveis para todos os países que são membros de um grupo de renda específico, escolhido pelo usuário. Os grupos de renda e seus membros são aqueles classificados pelo Banco Mundial: baixa renda, renda média-baixa, renda média-alta e renda alta. Este último é dividido ainda em países de renda alta dentro e excluídos da OCDE. Dado o menor número de países incluídos no WIOD, a agregação por grupo de renda só está disponível para o EPWT. A aba 'por país' exibe dados para um país individual específico, escolhido pelo usuário. O painel como um todo inclui, portanto, cinco níveis distintos de agregação: para agregados de nível de país, esses são (1) global, (2) por grupo de renda e (3) abas por país, e para agregações de nível de indústria, esses são (4) global e (5) abas por país.

Para cada seção do painel, o usuário tem a opção de selecionar um intervalo de datas para filtrar os dados. Quando as observações estão disponíveis ao longo de todo o intervalo de datas selecionado, todas essas observações são apresentadas. Quando as observações não estão disponíveis ao longo de todo o intervalo de datas selecionado devido à escassez de dados disponíveis, todas as observações disponíveis dentro desse intervalo de datas são apresentadas. Observe que o WIOD contém apenas observações ao longo do período de 2000 a 2014, enquanto o EPWT contém observações para alguns (mas não todos) os países ao longo do período de 1950 a 2019.

Observações ausentes dentro do EPWT representam um problema ao agregar variáveis em nível global e de grupo de renda ao longo de determinados intervalos de datas, como indicamos acima. Quando um país não possui uma observação em alguns anos do intervalo de datas escolhido, mas contém observações em outros anos dentro do intervalo de datas escolhido, a inclusão desse país em uma taxa de lucro global ou de grupo de renda resultaria em variáveis agregadas que incluem um número diferente de países para diferentes anos dentro desse intervalo de datas. Portanto, o usuário pode escolher entre dois métodos de cálculo: um que inclui todas as observações disponíveis - e, como resultado, pode incluir diferentes números de países ao longo do intervalo de datas escolhido - e um que inclui apenas aqueles países que contêm observações em todos os anos do intervalo de datas escolhido, resultando assim em um número consistente de países incluídos nas variáveis agregadas durante toda a duração desse intervalo de datas. Embora alguns países não contenham observações no WIOD para determinadas indústrias, o WIOD contém pelo menos algumas observações para todos os países em cada ano ao longo do período de 2000 a 2014; portanto, quando o WIOD é selecionado, todos os países disponíveis são usados nos cálculos agregados em qualquer intervalo de datas selecionado.

As variáveis extraídas do EPWT e do WIOD estão em preços correntes das moedas locais. Para calcular agregados globais, as moedas locais devem ser convertidas em unidades comuns. O usuário pode escolher entre o uso de taxas de câmbio nominais e paridades de poder de compra (PPPs) para a conversão em dólares americanos [17].

[Nota 17]: Note que, devido à disponibilidade limitada de dados de PPP e taxas de câmbio, o uso desses fatores de conversão diminui o número de países disponíveis para a agregação global. O título de cada gráfico indica o número de países incluídos na taxa de lucro mundial.

Para cada um dos cinco painéis distintos no painel de controle - para os cinco níveis distintos de agregação listados acima - o painel exibe dois gráficos. O primeiro gráfico exibe uma série temporal da taxa de lucro ao longo do intervalo de datas selecionado para o nível de agregação escolhido. O segundo gráfico exibe a decomposição de médio prazo da taxa de lucro em dois componentes: a parcela de lucro e a razão entre produção e capital. O usuário tem a opção de exibir essas variáveis como uma série temporal ou como um gráfico de barras que mostra a taxa média anual de crescimento das duas variáveis, bem como a taxa de lucro, ao longo do intervalo de datas selecionado. Contanto que haja mais de dois anos selecionados no intervalo de datas, a taxa média de crescimento é calculada como o coeficiente de regressão dos mínimos quadrados ordinários do logaritmo da variável dada em relação a uma constante e a uma tendência linear de tempo. Se houver apenas dois anos selecionados, a taxa de crescimento é calculada diretamente.

O usuário tem a opção de exibir os seguintes tipos de linhas de tendência nos gráficos de série temporal: linear, loess, quadrática e cúbica. O usuário pode baixar qualquer gráfico exibido, com uma escolha de tipos de arquivo no painel lateral. O usuário também pode baixar os dados usados para gerar os gráficos no formato .csv, que inclui todas as observações disponíveis para a taxa de lucro, parcela de lucro e razão entre produção e capital ao longo do intervalo de datas selecionado para o nível de agregação escolhido.

7. Conclusão

Neste artigo, relatamos estimativas das taxas de lucro mundial para o período de 1960 a 2019. A série de taxas de lucro mundial foi construída pela agregação de taxas de lucro de nível de país e de nível de indústria para um grande grupo de países capitalistas. A agregação usa tanto taxas de câmbio nominais quanto PPP. Descobrimos que a série de taxas de lucro mundial exibe uma tendência linear geral negativa de 1960 a 2019. Nossos resultados geralmente demonstram tendências amplas semelhantes na taxa de lucro mundial, conforme calculado por Maito (2014) e Roberts (2015).

Usando uma análise de decomposição de médio prazo, constatamos que a queda na taxa de lucro mundial foi totalmente provocada por uma queda na razão entre produção e capital. O mesmo padrão é visível em dois subperíodos, de 1960 a 1980 e de 1981 a 2019, com a queda sendo muito mais acentuada no primeiro do que no segundo período. Em ambos os subperíodos, a queda na taxa de lucro mundial foi impulsionada por uma queda na razão entre produção e capital. A evidência apresentada neste artigo mostra que os problemas tecnológicos têm sido a principal causa da lucratividade decrescente no nível da economia mundial. São problemas tecnológicos que levaram a uma tendência decrescente na razão entre produção e capital mundial.

A distribuição regressiva de renda, ou seja, um aumento na parcela de lucro, sustentou a taxa de lucro. Na ausência da redistribuição regressiva de renda, a taxa de lucro mundial teria diminuído em maior magnitude. O fato de os problemas tecnológicos, a principal força do capitalismo, terem sido o principal contribuinte para a queda da taxa de lucro na economia capitalista mundial está em total consonância com os insights de Marx sobre a dinâmica contraditória do capitalismo.

Pesquisas futuras sobre a lucratividade mundial devem explorar várias questões pendentes. Qual foi a causa primária da queda na razão entre produção e capital em nível global? Embora esteja claro que as revoluções tecnológicas da informação conseguiram reverter a queda na razão entre produção e capital mundial por uma década ou duas no início dos anos 1990, esse efeito rapidamente se dissipou. Qual é a razão para isso? Por que o capitalismo não conseguiu manter a razão entre produção e capital em ascensão por mais tempo? Quais são as implicações da tendência decrescente na taxa de lucro mundial para a acumulação de capital global? Essas são algumas das questões que podem ser abordadas em pesquisas futuras.