GEORGE, Donald. Mathematical Modelling for Economists. Springer, 1988.
1. Modelos, teorias e método (1)
2. Cálculo de várias variáveis (9)
2.1 Introdução
2.2 Funções e funções inversas
2.3 Continuidade e derivadas
2.4 Funções de várias variáveis
2.5 Máximos, mínimos e pontos de sela
2.6 Convexidade e concavidade
2.7 Derivadas parciais e totais
3. Teoria de Kuhn-Tucker (35)
3.1 Introdução
3.2 Maximização e minimização sujeitas a restrições
3.3 Métodos de Kuhn-Tucker
3.4 Uma aplicação dos métodos de Kuhn-Tucker
3.5 Multiplicadores como preços sombra
3.6 Modelagem da empresa gerida pelos trabalhadores
4. Programação linear (49)
4.1 Introdução
4.2 Problemas primais e duais
4.3 Teoremas da dualidade
4.4 Outra aplicação
4.5 Métodos numéricos de solução
5. Álgebra linear (63)
5.1 Introdução
5.2 Equações lineares simultâneas
5.3 Autovalores e autovetores
5.4 O modelo Leontief aberto
5.5 Modelos Neo-Ricardianos
6. Equações diferenciais (82)
6.1 Introdução
6.2 Equações diferenciais simples
6.3 Sistemas dinâmicos lineares bidimensionais
6.4 Sistemas dinâmicos lineares de maior dimensão
6.5 Linearização
6.6 Estabilidade estrutural e robustez
6.7 Dinâmica das expectativas racionais
7. Otimização dinâmica (113)
7.1 Introdução
7.2 O modelo de crescimento neoclássico de um setor
7.3 Um maximando mais geral
7.4 O princípio do máximo de Pontryagin
7.5 Um exemplo da economia da exaustão de recursos
7.6 Dinâmica das expectativas racionais revisitada
7.7 O critério de ultrapassagem
8. Descontinuidades e catástrofes (135)
8.1 Introdução
8.2 Um modelo de preferência por estado com não-convexidades
8.3 Teorema de Thorn
8.4 Um modelo de ciclo de comércio
8.5 Problemas metodológicos
___________________________________________________________________________________
1. Modelos, teorias e método (1)
Considere um estudante de Economia apresentado com as seguintes relações matemáticas:
e suponha que lhe seja dito que as equações (1.1)-(1.5) implicam:
Provavelmente, ele ou ela não ficará particularmente esclarecido(a) por essa informação. Agora, suponha que as variáveis nas equações (1.1)-(1.5) sejam simplesmente renomeadas da seguinte forma:
O conhecido modelo keynesiano da determinação da renda agregada agora se torna evidente e a equação (1.6) produz o resultado bem conhecido relacionando o multiplicador de investimento dY/dl à propensão marginal a consumir (a):
As equações (1.1)-(1.6) constituem um modelo matemático simples de determinação da renda agregada. O modelo consiste em várias relações matemáticas (equações (1.1)-(1.5)) juntamente com uma conclusão (equação (1.6)) deduzida delas de maneira matematicamente correta. As equações (1.1')-(1.6') simplesmente duplicam esse modelo, mas, usando nomes de variáveis mais sugestivos, tornam mais fácil de entender. Um modelo matemático, então, é um conjunto de relações matemáticas, chamadas de suposições, juntamente com algumas conclusões, corretamente deduzidas delas. É uma construção puramente lógica, sem significado empírico. Isso é ilustrado acima ao expressar o conhecido modelo Keynesiano de forma não convencional. Para adquirir significado empírico, um modelo requer interpretação. Por exemplo, a variável x na equação (1.1) pode ser renomeada como 'C na equação (1.1') e interpretada como 'consumo agregado', conforme medido por alguma estatística no 'Blue Book'. A equação (1.3) ou (1.3') pode ser interpretada como uma identidade contábil.
Onde Y = renda nacional
S = poupança
Uma identidade é uma equação (às vezes escrita com o símbolo ≡ em vez do símbolo igual usual =) que é verdadeira por definição de suas variáveis. Assim, a equação (1.3') é uma identidade porque a poupança é definida como a renda que não é consumida.
A interpretação não se limita à suposição de um modelo, estende-se também às conclusões. Os estudantes de economia estarão familiarizados com várias dificuldades associadas à interpretação da equação (1.6) ou (1.6'). Certamente, isso não significa que um aumento de £1 bilhão no GDCF hoje levará a um aumento de 11(1-α) x £1 bilhão no PIB amanhã.
Um modelo, então, pode ser pensado como o núcleo lógico de uma teoria. Suas suposições são derivadas por meio de um processo de abstração. Ou seja, o problema do "mundo real" a ser analisado é simplificado e suas características-chave são expressas matematicamente. As suposições de um modelo e, em particular, o que constitui uma "característica-chave" do mundo real, dependerão claramente da posição teórica do modelador. Criticar um modelo por omitir algum aspecto do "mundo real" é sempre um procedimento vazio, pois todos os modelos envolvem abstração e, portanto, a omissão de algum aspecto do problema do mundo real. O que é incluído e o que não é incluído em um modelo dependerá da posição teórica do modelador e do propósito para o qual o modelo está sendo construído. Esse último ponto pode ser ilustrado considerando os modelos não matemáticos construídos em outra disciplina: engenharia aeroespacial. É prática padrão construir modelos físicos de novas aeronaves e colocá-los em túneis de vento para testar suas propriedades aerodinâmicas. Esses testes de forma alguma são prejudicados pela omissão da cor do uniforme da comissária de bordo.
As suposições de um modelo são derivadas de um processo de abstração que é certamente seletivo e que reflete o ponto de vista teórico do modelador. Após declarar as suposições do modelo, um teste imediato de sua validade pode ser aplicado. As suposições devem ser mutuamente consistentes, ou seja, deve ser possível que todas sejam verdadeiras simultaneamente. A consistência é essencial, pois a partir de suposições inconsistentes, é possível derivar qualquer proposição, como a ideia de que a Lua é feita de queijo ou que cangurus jogam tênis, por exemplo.
Em segundo lugar, pode-se insistir que pelo menos algumas das variáveis no modelo possam ser interpretadas como grandezas empiricamente mensuráveis. Isso não precisa ser verdade para todas as variáveis. Em um modelo de maximização de utilidade de comportamento do consumidor, por exemplo, é difícil ver como a própria utilidade pode ser medida, embora a elasticidade da demanda (de mercado) possa muito bem ser. Muitas vezes, o requisito de mensurabilidade é imposto às variáveis das conclusões do modelo, embora não necessariamente às de suas suposições. Isso ocorre porque muitos economistas buscam testar as conclusões de um modelo, mas não necessariamente suas suposições. Esse ponto será retomado mais adiante.
Em terceiro lugar, é necessário exigir que as conclusões do modelo sejam deduzidas de suas suposições de maneira matematicamente correta.
A arte da construção de modelos, portanto, consiste em abstração, dedução e interpretação. A maior parte deste livro trata da dedução; ou seja, da derivação matematicamente correta de conclusões a partir de suposições. É aqui que a aplicação cuidadosa da matemática é essencial. No entanto, os outros aspectos da modelagem não são omitidos e, na prática, são tão importantes quanto a dedução de conclusões a partir de suposições.
O processo de modelagem tem o mérito de impor precisão ao economista. Ele ou ela é obrigado a fazer uma declaração precisa das suposições e mostrar precisamente como suas conclusões decorrem delas. Wicksteed (1894) certamente via o argumento matemático como oferecendo vantagens sobre métodos menos precisos:
A forma matemática da declaração atua como uma salvaguarda contra suposições inconscientes e como um reagente que precipitará as suposições mantidas em solução na verborragia de nossas disquisições comuns.
No entanto, tipicamente haverá um número infinito de modelos consistentes com qualquer teoria dada, e a escolha de qual modelo desenvolver deve ser uma questão de julgamento.
Pode-se legitimamente perguntar se a modelagem matemática contribui para o progresso na Economia, se tem algum propósito real. A abordagem matemática certamente contribuiu substancialmente em ciências naturais como a Física, mas talvez se possa ser menos certo sobre as ciências sociais, como a Economia. Tem sido sugerido que a análise matemática difícil fornece uma eficaz "barreira de entrada" para a disciplina da economia, permitindo que os economistas escondam ideias relativamente simples sob um formalismo impenetrável. Muitos estudantes, solicitados a ler três artigos da Econometrica até terça-feira seguinte, têm chegado a concordar com essa visão. Em seu livro "Vida entre os Econ" (1981), Axel Leijonhufvud compara os economistas a uma tribo (os "Econ"), da qual os "Math-Econ" formam a "casta sacerdotal". A importância dos modelos para os Econ é substancial, de acordo com Leijonhufvud:
"Os fatos (a) de que os Econ são altamente motivados pelo status, (b) que o status só pode ser alcançado criando "modis" e (c) que a maioria desses "modis" parece ter pouco ou nenhum uso prático, provavelmente explicam o atraso e a pobreza cultural da tribo...
... O surgimento dos Math-Econ parece estar associado à tendência anteriormente observada entre todos os Econ em direção a modis mais ornamentados e cerimoniais..."
Para alguns economistas, parece que a Economia deve adotar métodos matemáticos simplesmente porque lida com questões quantitativas. Essa visão parece ser independente de qualquer noção de modelagem. Jevons (1965), por exemplo, é bastante claro sobre a importância da matemática:
"É claro que a Economia, se deve ser uma ciência, deve ser uma ciência matemática. Existe muito preconceito contra tentativas de introduzir os métodos e a linguagem da matemática em qualquer ramo das ciências morais. Muitas pessoas parecem pensar que as ciências físicas formam o domínio do método matemático e que as ciências morais demandam algum outro método - não sei qual. Minha teoria da Economia, no entanto, é puramente de caráter matemático. Acredito que as quantidades com as quais lidamos devem estar sujeitas a variações contínuas, e não hesito em usar o ramo apropriado da ciência matemática, mesmo que isso envolva a consideração destemida de quantidades infinitesimalmente pequenas. A teoria consiste em aplicar o cálculo diferencial às noções familiares de riqueza, utilidade, valor, demanda, oferta, capital, juros, trabalho e todas as outras noções quantitativas que pertencem à operação diária da indústria. Assim como a teoria completa de quase todas as outras ciências envolve o uso desse cálculo, não podemos ter uma verdadeira teoria da economia sem a sua ajuda.
Para mim, parece que nossa ciência deve ser matemática simplesmente porque lida com quantidades."
Para alguns economistas, parece que a adoção de uma abordagem de modelagem matemática confere um viés ideológico ou político à Economia, uma vez que os métodos matemáticos parecem mais adequados a algumas perspectivas teóricas do que a outras. A aplicação do cálculo para desenvolver as ideias dos marginalistas é talvez um exemplo. Alguns marxistas ocidentais sugeriram que a abordagem matemática é inadequada para o desenvolvimento de ideias marxistas, apesar das tentativas de Morishima (1973) e Steedman (1977), entre outros, de 'matematizar Marx'. No entanto, o Nobel soviético L.V. Kantorovich (1959) tem a seguinte visão:
"Igualmente injustificado é o preconceito contra métodos matemáticos devido ao seu uso parcial por escolas econômicas burguesas. Claramente, os precedentes do uso incorreto da matemática para fins diferentes dos nossos não podem impedir os cientistas soviéticos de usar métodos matemáticos em problemas econômicos de maneira correta e vantajosa na construção do comunismo."
Seria tolo negar que economistas individuais têm viés político e ideológico, mas é difícil ver como a modelagem matemática em si impõe tal viés. No entanto, deve-se tratar os problemas econômicos e não os métodos matemáticos como primordiais e desenvolver modelos de acordo com isso. Ideias econômicas não devem ser rejeitadas ou ignoradas simplesmente porque parecem difíceis de capturar com técnicas de modelagem padrão. Pode ser necessário desenvolver novas técnicas, talvez utilizando ramos inovadores da matemática.
Até agora, temos mantido uma distinção entre modelos e teorias. Alguns economistas postulam uma relação muito próxima entre os dois. Aceitando o papel dos modelos em tornar precisa a relação entre suposições e conclusões, Koopmans (1957) argumenta que devemos:
Encare a teoria econômica como uma sequência de modelos conceituais que buscam expressar, em forma simplificada, diferentes aspectos de uma realidade sempre mais complexa. Inicialmente, esses aspectos são formalizados o máximo possível de forma isolada e, em seguida, em combinações de crescente realismo. Cada modelo é definido por um conjunto de postulados, cujas implicações são desenvolvidas na medida considerada válida em relação aos aspectos da realidade expressos pelos postulados. O estudo dos modelos mais simples é protegido da acusação de irrealidade pela consideração de que esses modelos podem ser protótipos de modelos subsequentes mais realistas, mas também mais complicados. O arquivo de peças de raciocínio bem-sucedidas representadas por esses modelos pode, então, ser visto como o núcleo lógico da economia, como o depósito da teoria econômica disponível.
Provavelmente é útil manter uma distinção mais nítida entre modelos e teorias. Um modelo, como foi dito, é uma construção puramente lógica, enquanto uma teoria consiste em um conjunto coerente de hipóteses com conteúdo empírico (ou "sintético"), projetado para fornecer explicações de fenômenos observáveis. Às vezes, argumenta-se que a importância dos modelos está em seu papel na teste de teorias. Os modelos podem ser construídos de forma a incorporar certas hipóteses de uma teoria e aplicá-las a um problema específico. Pode muito bem ser o caso que as conclusões de um modelo sejam mais fáceis de testar do que suas suposições. Assim, os modelos fornecem um elo crucial na aplicação e teste de teorias. Naturalmente, existe considerável debate sobre se deve-se testar as hipóteses de uma teoria ou suas previsões. Essa controvérsia está além do escopo deste livro, mas o leitor interessado a encontrará abordada nas referências mencionadas na seção de "leituras adicionais" no final do capítulo.
De qualquer forma, pode-se ver um papel para os modelos na avaliação de teorias com base nos motivos discutidos implicitamente na citação acima de Jevons, de que a maioria dos procedimentos de teste é quantitativa. Assim, uma função dos modelos na economia moderna é fornecer uma ligação entre as hipóteses da teoria e os dados da econometria.
O papel dos modelos na avaliação de teorias levanta uma questão importante pouco discutida na literatura. Dado que as suposições de um modelo são abstrações, é improvável que sejam exatamente verdadeiras, mas sim, espera-se que sejam aproximações razoáveis da realidade.
Nessas circunstâncias, é importante que as conclusões do modelo sejam robustas com relação a pequenas variações em suas suposições. Pequenas variações nessas suposições devem produzir apenas pequenas variações em suas conclusões, não variações selvagens e dramáticas. Sem essa propriedade de robustez, os testes empíricos de teorias se tornam impossíveis. Na verdade, observações significativas de qualquer tipo podem se tornar impossíveis devido a perturbações ambientais "aleatórias" nas condições sob as quais as observações são feitas. Considere uma teoria química que prevê o resultado de uma reação química específica em condições de temperatura ambiente constante. Não importa quão cuidadoso o químico experimental seja, ele não será capaz de manter a temperatura ambiente exatamente constante, ela está destinada a flutuar ligeiramente durante o curso do experimento. Suponha agora que o resultado do experimento seja substancialmente diferente do que a teoria previu. A teoria está refutada? O teórico pode sempre argumentar que a temperatura ambiente não era exatamente constante, como sua teoria exigia, e, portanto, o experimento não constitui uma refutação. Isso não aconteceria se a propriedade de robustez, discutida acima, tivesse sido exigida da teoria desde o início.
Essa propriedade de robustez acaba sendo de particular interesse no contexto de modelos dinâmicos, ou seja, modelos nos quais o tempo entra de alguma forma essencial. Tais modelos são frequentemente construídos usando a matemática de equações diferenciais e de diferenças. Portanto, a robustez é discutida de forma mais formal nos Capítulos 6 e 8. Baumol (1958) destaca a importância desse problema no contexto de modelos de equações de diferenças lineares do ciclo de comércio. Aqui, o problema é que ciclos persistentes e regulares ocorrem apenas para determinados valores exatos dos parâmetros. Perturbações arbitrariamente pequenas nesses parâmetros induzem uma transformação para ciclos amortecidos ou explosivos. O argumento de Baumol (1958) é o seguinte:
"Mas nossas estatísticas nunca são precisas o suficiente para distinguir uma raiz unitária (da equação característica de uma equação de diferenças linear) de uma que assume valores muito próximos dela... geralmente é possível mostrar que uma pequena alteração em uma das suposições simplificadoras eliminará as raízes unitárias e terá efeitos qualitativos profundos no sistema. Como Solow observou, uma vez que nossas premissas são sempre necessariamente mais ou menos falsas, um bom raciocínio consiste em grande parte em evitar suposições como essas, onde uma pequena mudança no que é pressuposto afetará seriamente as conclusões."
Como é bem conhecido, a resolução dessas dificuldades foi encontrada eventualmente por Hicks (1950), Goodwin (1951) e Desai (1973), entre outros, em modelos não lineares do ciclo de comércio.
A modelagem matemática, portanto, trata da abstração, dedução e interpretação. O restante deste livro explica várias ideias matemáticas que têm sido úteis na formulação de modelos econômicos. Também discute a aplicação da matemática a modelos específicos, bem como problemas de interpretação. A modelagem matemática, assim como a matemática, é um esporte participativo e não de espectador. O leitor é incentivado a seguir cuidadosamente os exemplos e tentar os exercícios (algumas respostas são fornecidas no Apêndice). Depois de fazê-lo, ele ou ela deve se sentir menos tentado a pular a "parte matemática complicada" em artigos de revistas e talvez seja estimulado a construir novos modelos, talvez até superar os da literatura existente.
Leituras adicionais
Katouzian (1980), Stewart (1979) e Blaug (1980) tratam de questões de metodologia econômica. Grande parte de Koopmans (1957) está preocupada com o papel da matemática na economia. Popper (1959) e Kuhn (1970) são referências clássicas sobre metodologia científica em geral. Covick (1974) satiriza a construção de modelos, enquanto Leijonhufvud (1981) compara os economistas a uma tribo primitiva para quem os modelos são objetos sagrados.
2 Cálculo de várias variáveis
2.1 Introdução
O objetivo deste capítulo é desenvolver certos aspectos do cálculo diferencial a partir do caso de funções de uma variável, familiar da matemática escolar, para funções de várias variáveis. Juntamente com a álgebra linear, assunto do Capítulo 5, o cálculo diferencial é uma ferramenta padrão para a construção de modelos em economia, e métodos de cálculo são usados em uma variedade de aplicações diferentes na economia. Um grupo particularmente grande de problemas nos quais os métodos de cálculo se manifestam é a classe de problemas que envolve a maximização de alguma função. Edgeworth (1881) tinha a visão de que:
"As principais investigações em Ciências Sociais podem ser vistas como problemas de maximização. Pois a Economia investiga os acordos entre agentes, cada um tendendo à sua própria utilidade máxima, e a Política e a Ética (Utilitária) investigam os acordos que conduzem à soma total máxima de utilidade. Uma vez que, então, as Ciências Sociais, em comparação com o Cálculo de Variações, partem de dados semelhantes - relações quantitativas soltas - e chegam a uma conclusão semelhante - determinação do máximo - por que não deveriam seguir o mesmo método, a Matemática?"
2.2 Funções e funções inversas
Da matemática escolar, a noção de função será familiar. A maioria das funções com as quais o leitor lidou provavelmente foi de funções reais de uma única variável real. Tal função (f) é frequentemente representada da seguinte forma:
é uma função se: f(x) existe e é única para cada x ∈ D.
Definição 2.2
O conjunto
R = {y ∈ C: y = f(x) para algum x ∈ D}
é chamado de alcance (ou imagem) da função f.
Estritamente falando, a especificação de uma função deve incluir a especificação do domínio e do contradomínio. Isso pode ser importante ao procurar a inversa de uma função.
Definição 2.3
Seja
f: D → C
então uma função inversa de f é uma função denominada
tal que
No entanto, isso não é uma função de ℝ para ℝ, uma vez que números positivos têm duas raízes quadradas (por exemplo, √4 = ±2) e números negativos não têm nenhuma. Isso é ilustrado na Figura 2.1, que mostra um gráfico da função f. No entanto, o domínio e o contradomínio de f podem ser reformulados:
onde ℝ+ denota os números reais positivos (incluindo zero). A equação (2.3) agora especifica uma função genuína, uma vez que cada número real positivo tem exatamente uma raiz quadrada positiva. O gráfico de f com domínio e contradomínio restritos é simplesmente o quadrante superior direito da Figura 2.1.
2.3 Continuidade e derivadas
O gráfico de f, representado na Figura 2.1, pode ser desenhado sem retirar a caneta do papel. Uma função assim é considerada contínua. Uma função contínua, em termos gerais, não apresenta saltos: ou seja, em qualquer ponto a no domínio, é possível obter f(x) tão próximo de f(a) quanto se desejar, escolhendo um x suficientemente próximo de a.
Para funções de variável real com valores reais, a definição formal é a seguinte.
Definição 2.4
Uma função:
$f: \mathbb{R}\rightarrow \mathbb{R}$
é considerada contínua em a ∈ ℝ se, para qualquer ε > 0, existir δ > 0 tal que
|x - a| < δ ⇒ |f(x) - f(a)| < ε
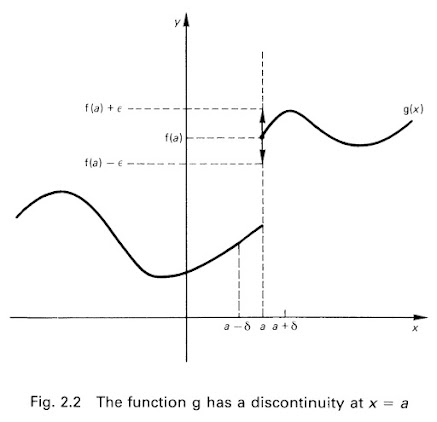
Considere uma função g que tem um salto, como mostrado na Figura 2.2. Para o valor de ε mostrado na Figura 2.2, nenhuma escolha de δ pode ser para satisfazer a condição da Definição 2.4. Portanto, a função g tem uma descontinuidade em x = a. As funções com as quais lidamos na economia geralmente são contínuas, mas, como veremos no Capítulo 8, certos tipos de descontinuidades podem ser importantes em modelos econômicos.
Figura 2.2 - A função g tem uma descontinuidade em x = a.
Equações: